Середньоарифметичне значення чисел. Середні величини у статистиці

Як порахувати середнє значення чисел в Excel

Знайти середнє арифметичне чисел в Excel можна за допомогою функції .

Синтаксис СРЗНАЧ

=СРЗНАЧ(число1;[число2];…) – російська версія

Аргументи СРЗНАЧ

число1– перше число чи діапазон чисел, до розрахунку середнього арифметичного;
число2(Опціонально) – друге число чи діапазон чисел розрахунку середнього арифметичного. Максимальна кількість аргументів функції – 255.

Для розрахунку виконайте такі кроки:

Виділіть будь-яку комірку;
Напишіть у ній формулу =СРЗНАЧ(
Виділіть діапазон осередків, для якого потрібно зробити розрахунок;
Натисніть клавішу “Enter” на клавіатурі

Функція розрахує середнє значення у вказаному діапазоні серед тих осередків, у яких є числа.

Як знайти середнє значення з урахуванням тексту

Якщо в діапазоні даних є порожні рядки або текст, функція сприймає їх як “нуль”. Якщо серед даних є логічні вислови Брехня або ІСТИНА, то Брехня функція сприймає як "нуль", а ІСТИНА як "1".

Як знайти середнє арифметичне за умовою

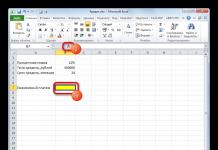
Для розрахунку середнього за умовою чи критерієм використовується функція. Наприклад, уявимо, що у нас є дані з продажу товарів:

Наше завдання – обчислити середнє значення продажів ручок. Для цього зробимо такі кроки:

У осередку A13напишемо назву товару "Ручки";
У осередку B13введемо формулу:

=ЗНАЧАЛЬНІ(A2:A10;A13;B2:B10)

Діапазон осередків “ А2: A10” вказує на список товарів, у якому ми шукатимемо слово “Ручки”. Аргумент A13це посилання на комірку з текстом, який ми шукатимемо серед усього списку товарів. Діапазон осередків “ B2: B10” це діапазон з даними продажу товарів, серед яких функція знайде “Ручки” та обчислить середнє значення.

Цей термін має й інші значення, див. середнє значення.

Середнє арифметичне(В математиці та статистиці) безлічі чисел - сума всіх чисел, поділена на їх кількість. Є одним із найпоширеніших заходів центральної тенденції.

Запропонована (поряд із середнім геометричним та середнім гармонійним) ще піфагорійцями.

Приватними випадками середнього арифметичного є середня (генеральна сукупність) і вибіркова середня (вибірки).

Вступ

Позначимо безліч даних X = (x 1 , x 2 , …, x n), тоді вибіркове середнє зазвичай позначається горизонтальною рисою над змінною (x ¯ (\displaystyle (\bar (x))) ), вимовляється « xз межею»).

Для позначення середнього арифметичного усієї сукупності використовується грецька буква μ. Для випадкової величини, на яку визначено середнє значення, μ є імовірнісне середнєчи математичне очікування випадкової величини. Якщо безліч Xє сукупністю випадкових чисел з імовірнісним середнім μ, тоді для будь-якої вибірки x iіз цієї сукупності μ = E( x i) є математичне очікування цієї вибірки.

На практиці різниця між μ і x ¯ (\displaystyle (\bar(x))) у тому, що μ є типовою змінною, тому що бачити можна швидше вибірку, а не всю генеральну сукупність. Тому, якщо вибірку представляти випадковим чином (у термінах теорії ймовірностей), тоді x (\displaystyle (bar (x))) (але не μ) можна трактувати як випадкову змінну, що має розподіл ймовірностей на вибірці (імовірнісний розподіл середнього).

Обидві ці величини обчислюються тим самим способом:

X = 1 n ∑ i = 1 n x i = 1 n (x 1 + ⋯ + x n) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+cdots +x_(n)).)

Якщо X- Випадкова змінна, тоді математичне очікування Xможна розглядати як середнє арифметичне значень у вимірах величини, що повторюються X. Це є виявом закону великих чисел. Тому вибіркове середнє використовується з метою оцінки невідомого математичного очікування.

В елементарній алгебрі доведено, що середня n+ 1 чисел більше середнього nчисел тоді і тільки тоді, коли нове число більше ніж старе середнє, менше тоді і тільки тоді, коли нове число менше середнього, і не змінюється тоді і лише тоді, коли нове число дорівнює середньому. Чим більше n, тим менше різницю між новим і старим середніми значеннями.

Зауважимо, що є кілька інших «середніх» значень, у тому числі середнє статечне, середнє Колмогорова, гармонійне середнє, арифметико-геометричне середнє та різні середньо-зважені величини (наприклад, середнє арифметичне зважене, середнє геометричне зважене, середнє гармонійне зважене).

Приклади

Для трьох чисел необхідно скласти їх і поділити на 3:

x 1 + x 2 + x 3 3 . (\displaystyle (\frac (x_(1)+x_(2)+x_(3))(3)).)

Для чотирьох чисел необхідно скласти їх і поділити на 4:

x 1 + x 2 + x 3 + x 4 4 . (\displaystyle (\frac (x_(1)+x_(2)+x_(3)+x_(4))(4)).)

Або простіше 5+5=10, 10:2. Тому що ми складали 2 числа, отже, скільки чисел складаємо, на стільки й ділимо.

Безперервна випадкова величина

Для безперервно розподіленої величини f(x) (displaystyle f(x)) середнє арифметичне на відрізку [ a ; b] (\displaystyle) визначається через певний інтеграл:

F (x) ¯ [ a ; b ] = 1 b − a ∫ a b f (x) d x (\displaystyle (\overline (f(x)))_()=(\frac (1)(b-a))\int _(a)^(b) f(x)dx)

Деякі проблеми застосування середнього

Відсутність боязкості

Основна стаття: Робастність у статистиці

Хоча середнє арифметичне часто використовується як середні значення або центральні тенденції, це поняття не відноситься до робастної статистики, що означає, що середнє арифметичне піддається сильному впливу «великих відхилень». Примітно, що для розподілів з великим коефіцієнтом асиметрії середнє арифметичне може не відповідати поняттю «середнього», а значення середнього з робастної статистики (наприклад, медіана) краще описувати центральну тенденцію.

Класичним прикладом є підрахунок середнього прибутку. Арифметичне середнє може бути неправильно витлумачено як медіану, через що може бути зроблено висновок, що людей з більшим доходом більше, ніж насправді. "Середній" дохід тлумачиться таким чином, що доходи більшості людей знаходяться поблизу цього числа. Цей «середній» (у сенсі середнього арифметичного) дохід є вищим, ніж доходи більшості людей, оскільки високий дохід з великим відхиленням від середнього робить сильний перекіс середнього арифметичного (на відміну від цього, середній дохід за медіаною «опирається» такому перекосу). Проте цей «середній» дохід нічого не говорить про кількість людей поблизу медіанного доходу (і не говорить нічого про кількість людей поблизу модального доходу). Проте, якщо легковажно поставитися до понять «середнього» і «більшість народу», можна зробити невірний висновок про те, що більшість людей мають доходи вищі, ніж вони є насправді. Наприклад, звіт про «середній» чистий доход у Медіні, штат Вашингтон, підрахований як середнє арифметичне всіх щорічних чистих доходів жителів, на подив велике число через Білла Гейтса. Розглянемо вибірку (1, 2, 2, 2, 3, 9). Середнє арифметичне дорівнює 3.17, але п'ять значень із шести нижче цього середнього.

Складний відсоток

Основна стаття: Окупність інвестицій

Якщо числа перемножувати, а не складатипотрібно використовувати середнє геометричне, а не середнє арифметичне. Найчастіше цей казус трапляється з розрахунку окупності інвестицій у фінансах.

Наприклад, якщо акції першого року впали на 10 %, а другий рік зросли на 30 %, тоді некоректно обчислювати «середнє» збільшення ці два роки як середнє арифметичне (−10 % + 30 %) / 2 = 10 %; правильне середнє значення у разі дають сукупні щорічні темпи зростання, якими річне зростання виходить лише близько 8,16653826392 % ≈ 8,2 %.

Причина цього в тому, що відсотки мають щоразу нову стартову точку: 30% – це 30% від меншого, ніж ціна на початку першого року, числа:якщо акції спочатку коштували $30 і впали на 10 %, вони на початку другого року коштують $27. Якщо акції зросли на 30%, вони наприкінці другого року коштують $35.1. Арифметичне середнє цього зростання 10%, але оскільки акції зросли за 2 роки лише на $5.1, середнє зростання у 8,2% дає кінцевий результат $35.1:

[$30 (1 – 0.1) (1 + 0.3) = $30 (1 + 0.082) (1 + 0.082) = $35.1]. Якщо ж використовувати так само середнє арифметичне значення 10 %, ми отримаємо фактичне значення: [$30 (1 + 0.1) (1 + 0.1) = $36.3].

Складний відсоток наприкінці 2 року: 90% * 130% = 117%, тобто загальний приріст 17%, а середньорічний складний відсоток 117% ≈ 108.2% (displaystyle (sqrt (117%)) approx 108.2%) тобто середньорічний приріст 8,2 %.

Напрями

Основна стаття: Статистика напрямків

При розрахунку середнього арифметичного значень певної змінної, що змінюється циклічно (наприклад, фаза або кут), слід виявляти особливу обережність. Наприклад, середнє чисел 1° і 359° дорівнюватиме 1 ∘ + 359 ∘ 2 = (displaystyle (\frac (1^(\circ )+359^(\circ ))(2))=) 180°. Це число неправильне з двох причин.

По-перше, кутові заходи визначені лише для діапазону від 0° до 360° (або від 0 до 2π при вимірі радіанах). Таким чином, ту ж пару чисел можна було б записати як (1 і -1) або як (1 і 719). Середні значення кожної з пар відрізнятимуться: 1 ∘ + (− 1 ∘) 2 = 0 ∘ (\displaystyle (\frac (1^(\circ )+(-1^(\circ ))))(2))=0 ^(\circ )) , 1 ∘ + 719 ∘ 2 = 360 ∘ (\displaystyle (\frac (1^(\circ )+719^(\circ ))(2))=360^(\circ )) .
По-друге, в даному випадку, значення 0° (еквівалентне 360°) буде геометрично кращим середнім значенням, оскільки числа відхиляються від 0° менше, ніж від будь-якого іншого значення (у значення 0° найменша дисперсія). Порівняйте:
- число 1° відхиляється від 0° лише на 1°;
- число 1° відхиляється від обчисленого середнього, що дорівнює 180°, на 179°.

Середнє значення для циклічної змінної, розраховане за наведеною формулою, буде штучно зрушено щодо справжнього середнього до середини числового діапазону. Через це середнє розраховується іншим способом, а саме, як середнє значення вибирається число з найменшою дисперсією (центральна точка). Також замість віднімання використовується модульна відстань (тобто відстань по колу). Наприклад, модульна відстань між 1° і 359° дорівнює 2°, а не 358° (на колі між 359° і 360°==0° - один градус, між 0° та 1° - теж 1°, у сумі - 2° °).

4.3. Середні величини. Сутність та значення середніх величин

Середньою величиноюв статистиці називається узагальнюючий показник, що характеризує типовий рівень явища в конкретних умовах місця і часу, що відображає величину ознаки, що варіює, у розрахунку на одиницю якісно однорідної сукупності. У економічній практиці використовують широке коло показників, обчислених як середніх величин.

Наприклад, узагальнюючим показником доходів робітників акціонерного товариства (АТ) служить середній дохід одного робітника, який визначається ставленням фонду заробітної плати та виплат соціального характеру за аналізований період (рік, квартал, місяць) до чисельності робітників АТ.

Обчислення середнього – один із поширених прийомів узагальнення; середній показник відображає те загальне, що характерно (типово) для всіх одиниць сукупності, що вивчається, в той же час він ігнорує відмінності окремих одиниць. У кожному явищі та його розвитку має місце поєднання випадковостіі необхідності.При обчисленні середніх через дію закону великих чисел випадковості взаємопогашуються, врівноважуються, тому можна абстрагуватися від несуттєвих особливостей явища, від кількісних значень ознаки у кожному даному випадку. У здатності абстрагуватися від випадковості окремих значень, коливань і укладена наукова цінність середніх як узагальнюючихпоказників сукупностей.

Там, де виникає потреба узагальнення, розрахунок таких характеристик призводить до заміни безлічі різних індивідуальних значень ознаки середнімпоказником, що характеризує всю сукупність явищ, що дозволяє виявити закономірності, властиві масовим суспільним явищам, непомітні у поодиноких явищах.

Середня відбиває характерний, типовий, реальний рівень досліджуваних явищ, характеризує ці рівні та його зміни у часі та просторі.

Середня - це зведена характеристика закономірностей процесу у умовах, у яких протікає.

4.4. Види середніх та способи їх обчислення

Вибір виду середньої визначається економічним змістом певного показника та вихідних даних. У кожному конкретному випадку застосовується одна з середніх величин: арифметична, гармонічна, геометрична, квадратична, кубічнаі т.д. Перераховані середні відносяться до класу статечнихсередніх.

Крім статечних середніх у статистичній практиці використовуються середні структурні, як яких розглядаються мода та медіана.

Зупинимося докладніше на статечних середніх.

Середня арифметична

Найбільш поширеним видом середніх є середня арифметична.Вона застосовується в тих випадках, коли обсяг ознаки, що варіює, для всієї сукупності є сумою значень ознак окремих її одиниць. Для суспільних явищ характерна адитивність (сумарність) обсягів варіюючої ознаки, цим визначається сфера застосування середньої арифметичної та пояснюється її поширеність як узагальнюючого показника, наприклад: загальний фонд заробітної плати – це сума заробітних плат усіх працівників, валовий збір урожаю – сума виробленої продукції з усієї посівної площі.

Щоб обчислити середню арифметичну, необхідно суму всіх значень ознак розділити з їхньої число.

Середня арифметична застосовується у формі простий середньої та виваженої середньої.Вихідною, визначальною формою служить проста середня.

Середня арифметична простадорівнює простій сумі окремих значень середньої ознаки, поділеної на загальне число цих значень (вона застосовується в тих випадках, коли є несгруповані індивідуальні значення ознаки):

де
- індивідуальні значення варіюючого (варіанти); м - Число одиниць сукупності.

Далі межі підсумовування у формулах не вказуватимуться. Наприклад, потрібно знайти середнє вироблення одного робітника (слюсаря), якщо відомо, скільки деталей виготовив кожен із 15 робочих, тобто. дано ряд індивідуальних значень ознаки, шт.:

21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.

Середня арифметична проста розраховується за формулою (4.1),1 шт.:

Середня з варіантів, які повторюються різне число разів, або, як кажуть, мають різну вагу, називається виваженою.Як ваги виступають чисельності одиниць у різних групах сукупності (у групу поєднують однакові варіанти).

Середня арифметична зважена- середня згрупованих величин, - обчислюється за формулою:

, (4.2)

де
- ваги (частоти повторення однакових ознак);

- сума творів величини ознак з їхньої частоти;

- загальна чисельність одиниць сукупності.

Техніку обчислення середньої арифметичної зваженої проілюструємо на розглянутому вище прикладі. Для цього згрупуємо вихідні дані та помістимо їх у табл. 4.1.

Таблиця 4.1

Розподіл робітників з вироблення деталей

За формулою (4.2) середня арифметична зважена дорівнює, шт.:

В окремих випадках ваги можуть бути не абсолютними величинами, а відносними (у відсотках або частках одиниці). Тоді формула середньої арифметичної зваженої матиме вигляд:

де
- Зокрема, тобто. частка кожної частоти у загальній сумі всіх

Якщо частоти підраховують у частках (коефіцієнтах), то
= 1,і формула середньої арифметично зваженої має вигляд:

Обчислення середньої арифметичної зваженої з групових середніх здійснюється за формулою:

де f-Кількість одиниць у кожній групі.

Результати обчислення середньої арифметичної із групових середніх представлені у табл. 4.2.

Таблиця 4.2

Розподіл робітників за середнім стажем роботи

У цьому прикладі варіантами є не індивідуальні дані про стаж роботи окремих робітників, а середні по кожному цеху. Терезами fє чисельності робітників у цехах. Звідси середній стаж роботи робітників по всьому підприємству становитиме:

Розрахунок середньої арифметичної в рядах розподілу

Якщо значення осредняемого ознаки задані як інтервалів («від - до»), тобто. інтервальних рядів розподілу, то при розрахунку середньої арифметичної величини як значень ознак у групах приймають середини цих інтервалів, у результаті утворюється дискретний ряд. Розглянемо наступний приклад (табл. 4.3).

Від інтервального ряду перейдемо до дискретного шляхом заміни інтервальних значень їх середніми значеннями/(проста середня

Таблиця 4.3

Розподіл робітників АТ за рівнем щомісячної оплати праці

Групи робітників по	Число робітників,	Середина інтервалу,
оплаті праці, руб.	чол., f	руб., х





900 і більше

величини відкритих інтервалів (перший та останній) умовно прирівнюються до інтервалів, що примикають до них (другий та передостанній).

При такому обчисленні середньої допускається певна неточність, оскільки робиться припущення про рівномірність розподілу одиниць ознаки всередині групи. Однак помилка буде тим меншою, чим уже інтервал і чим більше одиниць в інтервалі.

Після того, як знайдені середини інтервалів, обчислення роблять так само, як і в дискретному ряду, - варіанти множать на частоти (ваги) і суму творів ділять на суму частот (ваг), тис. руб.

Отже, середній рівень оплати праці робітників АТ становить 729 руб. на місяць.

Обчислення середньої арифметичної часто пов'язане з великими витратами часу та праці. Однак у ряді випадків процедуру розрахунку середньої можна спростити та полегшити, якщо скористатися її властивостями. Наведемо (без доказу) деякі основні властивості середньої арифметичної.

Властивість 1. Якщо всі індивідуальні значення ознаки (тобто. всі варіанти) зменшити або збільшити в iраз, то середнє значення нової ознаки відповідно зменшиться або збільшиться в iразів.

Властивість 2. Якщо всі варіанти ознаки, що осредняється, уміньшити або збільшити на число А, то середня арифметична відповідністьзменшиться або збільшиться на це ж число А.

Властивість 3. Якщо ваги всіх опосередкованих варіантів зменшити або збільшити в до раз, то середня арифметична не зміниться.

Як ваги середньої замість абсолютних показників можна використовувати питому вагу в загальному результаті (частки або відсотки). Тим самим досягається спрощення розрахунків середньої.

Для спрощення розрахунків середньої йдуть шляхом зменшення значень варіантів і частот. Найбільше спрощення досягається, коли як Авибирається значення одного з центральних варіантів, що має найбільшу частоту, як / - величина інтервалу (для рядів з однаковими інтервалами). Величина Л називається початком відліку, тому такий метод обчислення середньої називається «способом відліку від умовного нуля» або "способом моментів".

Припустимо, що всі варіанти хспочатку зменшені на те саме число А, а потім зменшені в iразів. Отримаємо новий варіаційний ряд розподілу нових варіантів .

Тоді нові варіантивисловлюватимуться:

а їхня нова середня арифметична , -момент першого порядку-формулою:

Вона дорівнює середньої з початкових варіантів, зменшеної спочатку на А,а потім у iразів.

Для отримання дійсної середньої потрібно момент першого порядку m 1 , помножити на iта додати А:

Даний спосіб обчислення середньої арифметичної з варіаційного ряду називають "способом моментів".Застосовується цей спосіб у рядах із рівними інтервалами.

Розрахунок середньої арифметичної за способом моментів ілюструється даними табл. 4.4.

Таблиця 4.4

Розподіл малих підприємств регіону за вартістю основних виробничих фондів (ОПФ) у 2000 р.

Групи підприємств за вартістю ВПФ, тис. руб.	Число підприємств, f	Середини інтервалів, x
14-16 16-18 18-20 20-22 22-24

Знаходимо момент першого порядку

Потім, приймаючи А = 19 і знаючи, що i= 2, обчислюємо х,тис. руб.:

Види середніх величин та методи їх розрахунку

На етапі статистичної обробки можуть бути поставлені різні завдання дослідження, для вирішення яких потрібно вибрати відповідну середню. При цьому необхідно керуватися наступним правилом: величини, які є чисельником і знаменником середньої, повинні бути логічно пов'язані між собою.

статечні середні;
структурні середні.

Введемо такі умовні позначення:

Величини, котрим обчислюється середня;

Середня, де риса зверху свідчить у тому, що має місце опосередкування індивідуальних значень;

Частота (повторність індивідуальних значень ознаки).

Різні середні виводяться із загальної формули статечної середньої:

(5.1)

при k = 1 – середня арифметична; k = -1 – середня гармонійна; k = 0 – середня геометрична; k = -2 – середня квадратична.

Середні величини бувають прості та зважені. Виваженими середніминазивають величини, які враховують, деякі варіанти значень ознаки може мати різну чисельність, у зв'язку з чим кожен варіант доводиться множити з цього чисельність. Інакше кажучи, «вагами» виступають числа одиниць сукупності у різних групах, тобто. кожен варіант "зважують" за своєю частотою. Частоту f називають статистичною вагоюабо вагою середньою.

Середня арифметична- Найпоширеніший вид середньої. Вона використовується, коли розрахунок здійснюється за несгрупованими статистичними даними, де потрібно отримати середній доданок. Середня арифметична - це середнє значення ознаки, при отриманні якого зберігається незмінним загальний обсяг ознаки в сукупності.

Формула середньої арифметичної ( простий) має вигляд

де n – чисельність сукупності.

Наприклад, середня заробітна плата працівників підприємства обчислюється як середня арифметична:

Визначальними показниками тут є заробітна плата кожного працівника та кількість працівників підприємства. При обчисленні середньої загальна сума заробітної плати залишилася колишньою, але розподіленою між усіма працівниками порівну. Наприклад, необхідно обчислити середню заробітну плату працівників невеликої фірми, де зайнято 8 осіб:

При розрахунку середніх величин окремі значення ознаки, що середня, можуть повторюватися, тому розрахунок середньої величини проводиться за згрупованими даними. У цьому випадку йдеться про використання середньої арифметичної зваженої, яка має вигляд

(5.3)

Так нам необхідно розрахувати середній курс акцій якогось акціонерного товариства на торгах фондової біржі. Відомо, що угоди здійснювалися протягом 5 днів (5 угод), кількість проданих акцій за курсом продажів розподілилася так:

1 – 800 ак. - 1010 руб.

2 - 650 ак. - 990 руб.

3 – 700 ак. - 1015 руб.

4 – 550 ак. - 900 руб.

5 – 850 ак. - 1150 руб.

Вихідним співвідношенням визначення середнього курсу вартості акцій є ставлення загальної суми угод (ОСС) до кількості проданих акцій (КПА).

Середнє арифметичне – статистичний показник, що демонструє середнє значення заданого масиву даних. Такий показник розраховується як дріб, у чисельнику якого коштує сума всіх значень масиву, а знаменнику - їх кількість. Середнє арифметичне – важливий коефіцієнт, який знаходить застосування у побутових розрахунках.

Сенс коефіцієнта

Середнє арифметичне - елементарний показник для порівняння даних та підрахунку прийнятного значення. Наприклад, у різних магазинах продається банку пива конкретного виробника. Але в одному магазині вона коштує 67 рублів, в іншому – 70 рублів, у третьому – 65 рублів, а в останньому – 62 рублі. Досить великий розбіг цін, тому покупцеві буде цікава середня вартість банки, щоб при купівлі товару міг порівняти свої витрати. У середньому банки пива по місту мають ціну:

Середня вартість = (67 + 70 + 65 + 62) / 4 = 66 рублів.

Знаючи середню ціну, легко визначити, де вигідно купувати товар, а де доведеться переплатити.

Середнє арифметичні постійно використовується у статистичних розрахунках у випадках, коли аналізується однорідний набір даних. У прикладі вище – це ціна банки пива однієї марки. Однак ми не можемо порівняти ціну на пиво різних виробників або ціни на пиво та лимонад, тому що в цьому випадку розкид значень буде більшим, середня ціна буде змащена і недостовірна, а сам сенс розрахунків спотвориться до карикатурного «середня температура по лікарні». Для розрахунку різнорідних масивів даних використовується середнє арифметичне зважене, коли кожне значення набуває свого вагового коефіцієнта.

Підрахунок середнього арифметичного

Формула для обчислень гранично проста:

P = (a1 + a2 + … an) / n,

де an - значення величини, n - загальна кількість значень.

Навіщо може використовуватися цей показник? Перше та очевидне його застосування – це статистика. Майже у кожному статистичному дослідженні використовується показник середнього арифметичного. Це може бути середній вік одруження в Росії, середня оцінка по предмету у школяра або середні витрати на продукти на день. Як говорилося вище, без урахування ваг підрахунок середніх значень може давати дивні чи абсурдні значення.

Наприклад, президент Російської Федерації заявив, що за статистикою, середня зарплата росіянина становить 27 000 рублів. Для більшості жителів Росії такий рівень зарплати видався абсурдним. Не дивно, якщо при розрахунку враховувати розмір доходів олігархів, керівників промислових підприємств, великих банкірів з одного боку та зарплати вчителів, прибиральників та продавців з іншого. Навіть середні зарплати за однією спеціальністю, наприклад, бухгалтера, матимуть серйозні відмінності у Москві, Костромі та Єкатеринбурзі.

Як рахувати середні для різнорідних даних

У ситуаціях із підрахунком заробітної плати важливо враховувати вагу кожного значення. Це означає, що зарплати олігархів та банкірів отримали б вагу, наприклад, 0,00001, а зарплати продавців – 0,12. Це цифри зі стелі, але вони приблизно ілюструють поширеність олігархів та продавців у суспільстві.

Таким чином, для підрахунку середнього або середнього значення в різнорідному масиві даних, потрібно використовувати середнє арифметичне зважене. Інакше ви отримаєте середню зарплату по Росії на рівні 27000 рублів. Якщо ж ви хочете дізнатися про свою середню оцінку з математики або середню кількість забитих шайб обраного хокеїста, то вам підійде калькулятор середнього арифметичного.

Наша програма є простий і зручний калькулятор для розрахунку середнього арифметичного. Для виконання розрахунків вам знадобиться ввести лише значення параметрів.

Розглянемо кілька прикладів

Розрахунок середньої оцінки

Багато вчителів використовують метод середнього арифметичного визначення річний оцінки по предмету. Давайте уявімо, що дитина отримала наступні четвертні позначки з математики: 3, 3, 5, 4. Яку річну оцінку йому поставить вчитель? Скористаємося калькулятором та порахуємо середнє арифметичне. Для початку оберіть відповідну кількість полів і введіть значення оцінок у комірки, що з'явилися:

(3 + 3 + 5 + 4) / 4 = 3,75

Вчитель округлить значення на користь учня, і школяр отримає за рік тверду четвірку.

Розрахунок з'їдених цукерок

Давайте проілюструємо деяку абсурдність середнього арифметичного. Уявімо, що Маша і Вови мали 10 цукерок. Маша з'їла 8 цукерок, а Вова – всього 2. Скільки цукерок у середньому з'їла кожна дитина? За допомогою калькулятора легко визначити, що в середньому діти з'їли по 5 цукерок, що зовсім не відповідає дійсності та здоровому глузду. Цей приклад показує, що показник середнього арифметичного важливо вважати для осмислених наборів даних.

Висновок

Розрахунок середнього арифметичного широко використовується у багатьох наукових сферах. Цей показник популярний у статистичних розрахунках, а й у фізиці, механіці, економіці, медицині чи фінансах. Використовуйте наші калькулятори як помічник для вирішення завдань на обчислення середнього арифметичного.

Найпоширенішим видом середньої є середня арифметична.

Середня арифметична проста

Проста середньоарифметична величина являє собою середній доданок, при визначенні якого загальний обсяг даної ознаки даних порівну розподіляється між усіма одиницями, що входять в дану сукупність. Так, середньорічне вироблення продукції на одного працюючого — це така величина обсягу продукції, яка припадала б на кожного працівника, якби весь обсяг випущеної продукції однаково розподілявся між усіма співробітниками організації. Середньоарифметична проста величина обчислюється за такою формулою:

Проста середня арифметична— дорівнює відношенню суми індивідуальних значень ознаки до кількості ознак у сукупності

Приклад 1 . Бригада з 6 робочих отримує місяць 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.

Знайти середню заробітну плату
Рішення: (3+3,2+3,3+3,5+3,8+3,1)/6 = 3,32 тис. руб.

Середня арифметична зважена

Якщо обсяг сукупності даних великий і є рядом розподілу, то обчислюється зважена середньоарифметична величина. Так визначають середньозважену ціну за одиницю продукції: загальну вартість продукції (суму творів її кількості на ціну одиниці продукції) поділяють на сумарну кількість продукції.

Подаємо це у вигляді наступної формули:

Зважена середня арифметична- дорівнює відношенню (суми творів значення ознаки до частоти повторення даної ознаки) до (сумі частот всіх ознак). Використовується, коли варіанти досліджуваної сукупності зустрічаються неоднакова кількість разів.

Приклад 2 . Знайти середню заробітну плату робітників цеху за місяць

Середня заробітна плата може бути отримана шляхом поділу загальної суми заробітної плати на загальну кількість робітників:

Відповідь: 3,35 тис.руб.

Середня арифметична для інтервального ряду

При розрахунку середньої арифметичної для інтервального варіаційного ряду спочатку визначають середню для кожного інтервалу, як напівсуму верхньої та нижньої меж, а потім середню всього ряду. У разі відкритих інтервалів значення нижнього або верхнього інтервалу визначається за величиною інтервалів, що примикають до них.

Середні обчислювані з інтервальних рядів є наближеними.

Приклад 3. Визначити середній вік студентів вечірнього осередку.

Середні обчислювані з інтервальних рядів є наближеними. Ступінь їх наближення залежить від того, якою мірою фактичний розподіл одиниць сукупності всередині інтервалу наближається до рівномірного.

При розрахунку середніх як терези можуть використовуватися не тільки абсолютні, а й відносні величини (частина):

Середня арифметична має цілу низку властивостей, які більш повно розкривають її сутність і спрощують розрахунок:

1. Твір середньої у сумі частот завжди дорівнює сумі творів варіант на частоти, тобто.

2.Середня арифметична суми величин, що варіюють, дорівнює сумі середніх арифметичних цих величин:

3.Алгебраїчна сума відхилень індивідуальних значень ознаки від середньої дорівнює нулю:

4.Сума квадратів відхилень варіантів від середньої менше, ніж сума квадратів відхилень від будь-якої іншої довільної величини, тобто.

Цей термін має й інші значення, див. середнє значення.

Запропонована (поряд із середнім геометричним та середнім гармонійним) ще піфагорійцями.

Вступ

Обидві ці величини обчислюються тим самим способом:

X = 1 n ∑ i = 1 n x i = 1 n (x 1 + ⋯ + x n) . (\displaystyle (\bar (x))=(\frac (1)(n))\sum _(i=1)^(n)x_(i)=(\frac (1)(n))(x_ (1)+cdots +x_(n)).)

Приклади

Для трьох чисел необхідно скласти їх і поділити на 3:

x 1 + x 2 + x 3 3 . (\displaystyle (\frac (x_(1)+x_(2)+x_(3))(3)).)

Для чотирьох чисел необхідно скласти їх і поділити на 4:

x 1 + x 2 + x 3 + x 4 4 . (\displaystyle (\frac (x_(1)+x_(2)+x_(3)+x_(4))(4)).)

Або простіше 5+5=10, 10:2. Тому що ми складали 2 числа, отже, скільки чисел складаємо, на стільки й ділимо.

Безперервна випадкова величина

F (x) ¯ [ a ; b ] = 1 b − a ∫ a b f (x) d x (\displaystyle (\overline (f(x)))_()=(\frac (1)(b-a))\int _(a)^(b) f(x)dx)

Деякі проблеми застосування середнього

Відсутність боязкості

Основна стаття: Робастність у статистиці

Складний відсоток

Основна стаття: Окупність інвестицій

Напрями

Основна стаття: Статистика напрямків

По-перше, кутові заходи визначені лише для діапазону від 0° до 360° (або від 0 до 2π при вимірі радіанах). Таким чином, ту ж пару чисел можна було б записати як (1 і -1) або як (1 і 719). Середні значення кожної з пар відрізнятимуться: 1 ∘ + (− 1 ∘) 2 = 0 ∘ (\displaystyle (\frac (1^(\circ )+(-1^(\circ ))))(2))=0 ^(\circ )) , 1 ∘ + 719 ∘ 2 = 360 ∘ (\displaystyle (\frac (1^(\circ )+719^(\circ ))(2))=360^(\circ )) .
По-друге, в даному випадку, значення 0° (еквівалентне 360°) буде геометрично кращим середнім значенням, оскільки числа відхиляються від 0° менше, ніж від будь-якого іншого значення (у значення 0° найменша дисперсія). Порівняйте:
- число 1° відхиляється від 0° лише на 1°;
- число 1° відхиляється від обчисленого середнього, що дорівнює 180°, на 179°.

Види середніх величин та методи їх розрахунку

статечні середні;
структурні середні.

Введемо такі умовні позначення:

Величини, котрим обчислюється середня;

Середня, де риса зверху свідчить у тому, що має місце опосередкування індивідуальних значень;

Частота (повторність індивідуальних значень ознаки).

Різні середні виводяться із загальної формули статечної середньої:

(5.1)

Формула середньої арифметичної ( простий) має вигляд

де n – чисельність сукупності.

Наприклад, середня заробітна плата працівників підприємства обчислюється як середня арифметична:

(5.3)

1 – 800 ак. - 1010 руб.

2 - 650 ак. - 990 руб.

3 – 700 ак. - 1015 руб.

4 – 550 ак. - 900 руб.

5 – 850 ак. - 1150 руб.

Вихідним співвідношенням визначення середнього курсу вартості акцій є ставлення загальної суми угод (ОСС) до кількості проданих акцій (КПА):

ОСС = 1010 · 800 +990 · 650 +1015 · 700 +900 · 550 +1150 · 850 = 3634500;

КПА = 800 +650 +700 +550 +850 = 3550.

У цьому випадку середній курс вартості акцій дорівнював

Необхідно знати властивості арифметичної середньої, що дуже важливо як щодо її використання, так і при її розрахунку. Можна виділити три основні властивості, які найбільше зумовили широке застосування арифметичної середньої статистико-економічних розрахунків.

Властивість перша (нульове): сума позитивних відхилень індивідуальних значень ознаки від його середнього значення дорівнює сумі негативних відхилень. Це дуже важлива властивість, оскільки вона показує, що будь-які відхилення (як з +, так і з -), спричинені випадковими причинами, будуть взаємно погашені.

Доказ:

Властивість друга (мінімальне): сума квадратів відхилень індивідуальних значень ознаки від середньої арифметичної менше, ніж будь-якого іншого числа (а), тобто. є мінімальне число.

Доказ.

Складемо суму квадратів відхилень від змінної а:

(5.4)

Щоб знайти екстремум цієї функції, необхідно її похідну а прирівняти нулю:

Звідси отримуємо:

(5.5)

Отже, екстремум суми квадратів відхилень досягається при . Цей екстремум – мінімум, тому що функція не може мати максимуму.

Властивість третя: середня арифметична постійної величини дорівнює цій постійній: при а = const.

Крім цих трьох найважливіших властивостей середньої арифметичної є так звані розрахункові властивості, які поступово втрачають свою значущість у зв'язку з використанням електронно-обчислювальної техніки:

якщо індивідуальне значення ознаки кожної одиниці помножити або розділити на постійне число, то середня арифметична збільшиться або зменшиться у стільки разів;
середня арифметична не зміниться, якщо вага (частоту) кожного значення ознаки поділити на постійне число;
якщо індивідуальні значення ознаки кожної одиниці зменшити або збільшити на ту саму величину, то середня арифметична зменшиться або збільшиться на ту саму величину.

Середня гармонійна. Цю середню називають зворотною середньою арифметичною, оскільки ця величина використовується при k = -1.

Проста середня гармонійнавикористовується тоді, коли ваги значень ознаки однакові. Її формулу можна вивести із базової формули, підставивши k = -1:

Наприклад, нам необхідно обчислити середню швидкість двох машин, що пройшли той самий шлях, але з різною швидкістю: перша - зі швидкістю 100 км/год, друга - 90 км/год. Застосовуючи метод середньої гармонійної, ми обчислюємо середню швидкість:

У статистичній практиці найчастіше використовується гармонійна зважена, формула якої має вигляд

Ця формула використовується у випадках, коли ваги (чи обсяги явищ) за кожним ознакою не рівні. У вихідному співвідношенні до розрахунку середньої відомий чисельник, але невідомий знаменник.

Наприклад, при розрахунку середньої ціни ми маємо користуватися ставленням суми реалізації до кількості реалізованих одиниць. Нам не відомо кількість реалізованих одиниць (йдеться про різні товари), але відомі суми реалізацій цих різних товарів. Допустимо, необхідно дізнатися середню ціну реалізованих товарів:

Отримуємо

Середня геометрична. Найчастіше середня геометрична знаходить своє застосування щодо середніх темпів зростання (середніх коефіцієнтів зростання), коли індивідуальні значення ознаки представлені як відносних величин. Вона використовується також, якщо необхідно знайти середню між мінімальним та максимальним значеннями ознаки (наприклад, між 100 та 1000000). Існують формули для простої та виваженої середньої геометричної.

Для простої середньої геометричної

Для виваженої середньої геометричної

Середня квадратична величина. Основною сферою її застосування є вимірювання варіації ознаки в сукупності (розрахунок середнього відхилення квадратичного).

Формула простої середньої квадратичної

Формула виваженої середньої квадратичної

(5.11)

У результаті можна сказати, що від правильного вибору виду середньої величини у кожному конкретному випадку залежить успішне вирішення завдань статистичного дослідження. Вибір середньої передбачає таку послідовність:

а) встановлення узагальнюючого показника сукупності;

б) визначення даного узагальнюючого показника математичного співвідношення величин;

в) заміна індивідуальних значень середніми величинами;

г) розрахунок середньої за допомогою відповідного рівняння.

Середні величини та варіація

Середня величина- це узагальнюючий показник, який характеризує якісно однорідну сукупність за певною кількісною ознакою. Наприклад, середній вік осіб, засуджених за крадіжку.

У судовій статистиці середні величини використовують для характеристики:

Середніх термінів розгляду справ цієї категорії;

Середній розмір позову;

Середньої кількості відповідачів, що припадають одну справу;

Середній розмір шкоди;

Середнє навантаження суддів, та ін.

Середня величина завжди іменована і має ту ж розмірність, що і ознака в окремої одиниці сукупності. Кожна середня величина характеризує досліджувану сукупність за якою-небудь однією ознакою, що варіює, тому за всякою середньою ховається ряд розподілу одиниць цієї сукупності за досліджуваною ознакою. Вибір виду середньої визначається змістом показника та вихідних даних для розрахунку середньої величини.

Усі види середніх величин, які у статистичних дослідженнях, поділяються на дві категорії:

1) статечні середні;

2) структурні середні.

Перша категорія середніх величин включає: середню арифметичну, середню гармонійну, середню геометричну і середню квадратичну . Друга категорія – це модаі медіана. При цьому кожен із перерахованих видів статечних середніх величин може мати дві форми: просту і зважену . Проста форма середньої величини використовується для отримання середнього значення ознаки, що вивчається, коли розрахунок здійснюється за несгрупованими статистичними даними, або коли кожна варіанта в сукупності зустрічається тільки один раз. Зваженими середніми називають величини, які враховують, що варіанти значень ознаки можуть мати різну чисельність, у зв'язку з чим кожен варіант доводиться множити на відповідну частоту. Іншими словами, кожен варіант зважують за своєю частотою. Частоту називають статистичною вагою.

Середня арифметична проста- Найпоширеніший вид середньої. Вона дорівнює сумі окремих значень ознаки, поділеної на загальну кількість цих значень:

де x 1, x 2, …, x N- Індивідуальні значення варіює ознаки (варіанти), а N - число одиниць сукупності.

Середня арифметична зваженазастосовується у тих випадках, коли дані представлені у вигляді рядів розподілу чи угруповань. Вона обчислюється як сума творів варіантів відповідні їм частоти, поділена у сумі частот всіх варіантів:

де x i– значення i-і варіанти ознаки; f i- Частота i-і варіанти.

Таким чином, кожне значення варіанти зважується за частотою, тому частоти іноді називають статистичними вагами.

Зауваження.Коли йдеться про середню арифметичну величину без зазначення її виду, мається на увазі середня арифметична проста.

Таблиця 12

Рішення.Для розрахунку використовуємо формулу середньої арифметичної зваженої:

Таким чином, у середньому на одну кримінальну справу припадає двоє обвинувачених.

Якщо обчислення середньої величини проводять за даними, згрупованими у вигляді інтервальних рядів розподілу, то спочатку треба визначити серединні значення кожного інтервалу х" i , після чого розрахувати середню величину за формулою середньої арифметичної зваженої, яку замість x i підставляють х" i .

приклад.Дані про вік злочинців, засуджених за скоєння крадіжки, наведено в таблиці:

Таблиця 13

Визначити середній вік злочинців, засуджених за вчинення крадіжки.

Рішення.Щоб визначити середній вік злочинців з урахуванням інтервального варіаційного ряду необхідно спочатку знайти серединні значення інтервалів. Так як дано інтервальний ряд з відкритими першим та останнім інтервалами, то величини цих інтервалів приймаються рівними величинам суміжних закритих інтервалів. У разі величина першого і останнього інтервалів дорівнюють 10.

Тепер знаходимо середній вік злочинців за формулою середньої арифметичної зваженої:

Таким чином, середній вік злочинців, засуджених за скоєння крадіжки, приблизно дорівнює 27 років.

Середня гармонійна проста являє собою величину, обернену до середньої арифметичної зі зворотних значень ознаки:

де 1/ x i– обернені значення варіантів, а N – число одиниць сукупності.

приклад.Для визначення середнього річного навантаження на суддів районного суду під час розгляду справ провели обстеження навантаження 5 суддів цього суду. Середні витрати часу на одну кримінальну справу для кожного з обстежених суддів виявились рівними (у днях): 6, 0, 5, 6, 6, 3, 4, 9, 5, 4. Знайти середні витрати на одну кримінальну справу та середнє річне навантаження на суддів цього районного суду під час розгляду кримінальних справ.

Рішення.Для визначення середніх витрат часу на одну кримінальну справу, скористаємося формулою середньої гармонійної простий:

Для спрощення розрахунків у прикладі візьмемо число днів у році рівним 365, включаючи вихідні (це не впливає на методику розрахунку, а при обчисленні аналогічного показника на практиці необхідно замість 365 днів підставити кількість робочих днів у конкретному році). Тоді середнє річне навантаження на суддів даного районного суду при розгляді кримінальних справ становитиме: 365(днів): 5,56 ≈ 65,6 (справ).

Якби ми для визначення середніх витрат часу на одну кримінальну справу, скористалися б формулою середньої арифметичної простої, то отримали б:

365 (днів): 5,64 ≈ 64,7 (справи), тобто. середнє навантаження на суддів виявилося меншим.

Перевіримо обґрунтованість такого підходу. Для цього скористаємося даними про витрати часу на одну кримінальну справу для кожного судді та розрахуємо кількість кримінальних, розглянутих кожним із них за рік.

Отримаємо відповідно:

365(днів) : 6 ≈ 61 (справа), 365(днів) : 5,6 ≈ 65,2 (справ), 365(днів) : 6,3 ≈ 58 (справ),

365(днів) : 4,9 ≈ 74,5 (справи), 365(днів) : 5,4 ≈ 68 (справ).

Наразі обчислимо середнє річне навантаження на суддів даного районного суду при розгляді кримінальних справ:

Тобто. середнє річне навантаження таке ж, як і при використанні середньої гармонійної.

Отже, використання середньої арифметичної у разі неправомірно.

У тих випадках, коли відомі варіанти ознаки, їх об'ємні значення (твір варіанти на частоту), але невідомі самі частоти, застосовується формула середньої зваженої гармонійної:

де x i– значення варіантів ознаки, а w i – об'ємні значення варіантів ( w i = x i · f i).

приклад.Дані про ціну одиниці однотипного товару, виробленого різними установами кримінально-виконавчої системи, та обсяги його реалізації наведено у таблиці 14.

Таблиця 14

Знайти середню ціну реалізації товару.

Рішення.При розрахунку середньої ціни ми маємо користуватися ставленням суми реалізації до кількості реалізованих одиниць. Нам невідомо кількість реалізованих одиниць, але відомі суми реалізації товарів. Тому для знаходження середньої ціни реалізованих товарів скористаємося формулою середньої гармонійної виваженої. Отримуємо

Якщо тут використовувати формулу середньої арифметичної, можна отримати середню ціну, яка буде нереальна:

Середня геометричнаобчислюється вилученням кореня ступеня N з добутку всіх значень варіантів ознаки:

де x 1, x 2, …, x N- індивідуальні значення варіюючої ознаки (варіанти), а

N- Число одиниць сукупності.

Цей вид середньої використовується обчислення середніх показників зростання рядів динаміки.

Середня квадратичназастосовується для розрахунку середньоквадратичного відхилення, що є показником варіації, та буде розглянуто нижче.

Для визначення структури сукупності використовують спеціальні середні показники, до яких належать медіана і мода , або звані структурні середні. Якщо середня арифметична розраховується з урахуванням використання всіх варіантів значень ознаки, то медіана і мода характеризують величину того варіанта, який займає певне середнє становище ранжированном (упорядкованому) ряду. Упорядкування одиниць статистичної сукупності може бути проведено за зростанням або зменшенням варіантів досліджуваної ознаки.

Медіана (Ме)- Це величина, яка відповідає варіанту, що знаходиться в середині ранжованого ряду. Таким чином, медіана - це той варіант ранжованого ряду, по обидва боки від якого в цьому ряду має знаходитися однакова кількість одиниць сукупності.

Для знаходження медіани спочатку необхідно визначити її порядковий номер у ранжованому ряду за формулою:

де N – обсяг низки (кількість одиниць сукупності).

Якщо ряд складається з непарного числа членів, то медіана дорівнює варіанті номером N Me . Якщо ряд складається з парного числа членів, то медіана визначається як середнє арифметичне двох суміжних варіант, розташованих у середині.

приклад.Даний ранжований ряд 1, 2, 3, 3, 6, 7, 9, 9, 10. Обсяг ряду N = 9, отже N Me = (9 + 1) / 2 = 5. Отже, Ме = 6, тобто . п'ятий варіант. Якщо дано ряд 1, 5, 7, 9, 11, 14, 15, 16, тобто. ряд з парною кількістю членів (N = 8), то N Me = (8 + 1) / 2 = 4,5. Отже медіана дорівнює напівсумі четвертої і п'ятої варіант, тобто. Ме = (9 + 11)/2 = 10.

У дискретному варіаційному ряду медіану визначають за накопиченими частотами. Частоти варіант, починаючи з першої, підсумовуються до тих пір, поки не буде перевищено номер медіани. Значення останньої підсумованої варіанти буде медіаною.

приклад.Знайти медіану числа обвинувачених, які припадають однією кримінальну справу, використовуючи дані таблиці 12.

Рішення.У разі обсяг варіаційного ряду N = 154, отже, N Me = (154 + 1) / 2 = 77,5. Підсумувавши частоти першої та другої варіанти, отримаємо: 75 + 43 = 118, тобто. ми перевершили номер медіани. Значить Ме = 2.

В інтервальному варіаційному ряду розподілу спочатку вказують інтервал, у якому буде медіана. Його називають медіанним . Це перший інтервал, накопичена частота якого перевищує половину обсягу інтервального варіаційного ряду. Потім чисельне значення медіани визначається за такою формулою:

де x Ме– нижня межа медіанного інтервалу; i – величина медіанного інтервалу; S Ме-1– накопичена частота інтервалу, що передує медіанному; f Ме- Частота медіанного інтервалу.

приклад.Знайти медіану віку злочинців, засуджених за скоєння крадіжки, з урахуванням статистичних даних, поданих у таблиці 13.

Рішення.Статистичні дані представлені інтервальним варіаційним рядом, отже спочатку визначимо медіанний інтервал. Обсяг сукупності N = 162, отже, медіанним інтервалом є 18-28, т.к. це перший інтервал, накопичена частота якого (15 + 90 = 105) перевищує половину обсягу (162: 2 = 81) інтервального варіаційного ряду. Тепер чисельне значення медіани визначаємо за наведеною вище формулою:

Таким чином, половина засуджених за скоєння крадіжки молодше 25 років.

Модою (Мо)називають значення ознаки, що найчастіше зустрічається в одиниць сукупності. До моди вдаються виявлення величини ознаки, що має найбільшого поширення. Для дискретного ряду модою буде варіант із найбільшою частотою. Наприклад, для дискретного ряду, поданого в таблиці 3 Мо= 1, оскільки цього значення варіанти відповідає найбільша частота - 75. Для визначення моди інтервального ряду спочатку визначають модальний інтервал (інтервал, що має найбільшу частоту). Потім у межах цього інтервалу знаходять значення ознаки, яке може бути модою.

Його значення знаходять за такою формулою:

де x Mo- нижня межа модального інтервалу; i – величина модального інтервалу; f Мо- Частота модального інтервалу; f Мо-1– частота інтервалу, що передує модальному; f Мо+1- Частота інтервалу, наступного за модальним.

приклад.Знайти моду віку злочинців, засуджених за скоєння крадіжки, дані про які представлені в таблиці 13.

Рішення.Найбільша частота відповідає інтервалу 18-28, отже, мода повинна бути в цьому іртервалі. Її величину визначаємо за наведеною вище формулою:

Таким чином, найбільше злочинців, засуджених за скоєння крадіжки, має вік 24 роки.

Середня величина дає узагальнюючу характеристику всієї сукупності явища, що вивчається. Однак дві сукупності, що мають однакові середні значення, можуть значно відрізнятися один від одного за рівнем коливання (варіації) величини ознаки, що вивчається. Наприклад, в одному суді було призначено такі строки позбавлення волі: 3, 3, 3, 4, 5, 5, 5, 12, 12, 15 років, а в іншому – 5, 5, 6, 6, 7, 7, 7 8, 8, 8 років. У обох випадках середня арифметична дорівнює 6,7 років. Однак ці сукупності суттєво різняться між собою розкидом індивідуальних значень призначеного терміну позбавлення волі щодо середнього значення.

І першого суду, де цей розкид досить великий, середня величина терміну позбавлення волі погано відбиває всю сукупність. Таким чином, якщо індивідуальні значення ознаки мало відрізняються один від одного, то середня арифметична буде досить показовою характеристикою властивостей цієї сукупності. В іншому випадку середня арифметична буде ненадійною характеристикою цієї сукупності та застосування її на практиці малоефективне. Тому необхідно враховувати варіацію значень ознаки, що вивчається.

Варіація- Це відмінності в значеннях будь-якої ознаки у різних одиниць даної сукупності в той самий період або момент часу. Термін «варіація» має латинське походження – variatio, що означає різницю, зміну, коливання. Вона виникає внаслідок того, що індивідуальні значення ознаки складаються під сукупним впливом різноманітних факторів (умов), які по-різному поєднуються у кожному окремому випадку. Для вимірювання варіації ознаки застосовуються різні абсолютні та відносні показники.

До основних показників варіації належать такі:

1) розмах варіації;

2) середнє лінійне відхилення;

3) дисперсія;

4) середнє квадратичне відхилення;

5) коефіцієнт варіації.

Стисло зупинимося на кожному з них.

Розмах варіації R найдоступніший за простотою розрахунку абсолютний показник, який визначається як різницю між найбільшим і найменшим значеннями ознаки у одиниць даної сукупності:

Розмах варіації (розмах коливань) – важливий показник коливання ознаки, але він дає можливість побачити лише крайні відхилення, що обмежує сферу його застосування. Для більш точної характеристики варіації ознаки з урахуванням урахування його коливання використовуються інші показники.

Середнє лінійне відхиленняє середнім арифметичним з абсолютних значень відхилень індивідуальних значень ознаки від середньої і визначається за формулами:

1) для несгрупованих даних

2) для варіаційного ряду

Однак найбільш широко застосовуваним показником варіації є дисперсія . Вона характеризує міру розкиду значень досліджуваного ознаки щодо його середнього значення. Дисперсія визначається як середня із відхилень, зведених у квадрат.

Проста дисперсіядля не згрупованих даних:

Зважена дисперсіядля варіаційного ряду:

Зауваження.Насправді для обчислення дисперсії краще використовувати такі формулы:

Для простої дисперсії

Для зваженої дисперсії

Середнє квадратичне відхилення- це корінь квадратний із дисперсії:

Середнє квадратичне відхилення є мірилом середньої надійності. Чим менше середнє квадратичне відхилення, тим, однорідніше сукупність і краще середня арифметична відбиває собою всю сукупність.

Розглянуті вище заходи розсіювання (розмах варіації, дисперсія, середнє квадратичне відхилення) є абсолютними показниками, судити з яких ступінь коливання ознаки який завжди можливо. У деяких завданнях необхідно використовувати відносні показники розсіювання, одним із яких є коефіцієнт варіації.

Коефіцієнт варіації- Виражене у відсотках відношення середнього квадратичного відхилення до середньої арифметичної:

Коефіцієнт варіації використовують як порівняльної оцінки варіації різних ознак чи однієї й тієї ж ознаки у різних сукупностях, але й характеристики однорідності сукупності. Статистична сукупність вважається кількісно однорідною, якщо коефіцієнт варіації вбирається у 33 % (для розподілів, близьких до нормального розподілу).

приклад.Є такі дані про терміни позбавлення волі 50 засуджених, доставлених для відбування призначеного судом покарання до виправної установи кримінально-виконавчої системи: 5, 4, 2, 1, 6, 3, 4, 3, 2, 2, 5, 6, 4, 3 , 10, 5, 4, 1, 2, 3, 3, 4, 1, 6, 5, 3, 4, 3, 5, 12, 4, 3, 2, 4, 6, 4, 4, 3, 1 5, 4, 3, 12, 6, 7, 3, 4, 5, 5, 3.

1. Побудувати низку розподілу за строками позбавлення волі.

2. Знайти середнє значення, дисперсію та середнє квадратичне відхилення.

3. Обчислити коефіцієнт варіації та зробити висновок про однорідність чи неоднорідність досліджуваної сукупності.

Рішення.Для побудови дискретного ряду розподілу необхідно визначити варіанти та частоти. Варіанта у цьому – це термін позбавлення волі, а частоти – чисельність окремих варіант. Розрахувавши частоти, отримаємо наступний дискретний ряд розподілу:

Знайдемо середнє значення та дисперсію. Оскільки статистичні дані представлені дискретним варіаційним рядом, то їх обчислення будемо використовувати формули середнього арифметичного зваженого і дисперсії. Отримаємо:

= = 4,1;

= 5,21.

Тепер обчислюємо середнє квадратичне відхилення:

Знаходимо коефіцієнт варіації:

Отже, статистична сукупність кількісно неоднорідна.

Середня арифметична проста

Середні величини

Велике поширення у статистиці мають середні величини.

Середня величина- це узагальнюючий показник, у якому виражаються дії загальних умов, закономірностей розвитку досліджуваного явища.

Статистичні середні розраховуються на основі масових даних правильно статистично організованого спостереження (суцільного та вибіркового). Однак статистична середня буде об'єктивною і типовою, якщо вона розраховується за масовими даними для якісно однорідної сукупності (масових явищ). Наприклад, якщо розраховувати середню заробітну плату в акціонерних товариствах і на держпідприємствах, а результат поширити на всю сукупність, то середня фіктивна, оскільки розрахована за неоднорідною сукупністю, і така середня втрачає будь-який сенс.

За допомогою середньої відбувається як би згладжування відмінностей у величині ознаки, що виникають з тих чи інших причин в окремих одиниць спостереження.

Наприклад, середнє вироблення окремого продавця залежить багатьох причин: кваліфікації, стажу, віку, форми обслуговування, здоров'я тощо. Середнє вироблення відбиває загальну характеристику всієї сукупності.

Середня величина вимірюється у тих самих одиницях, як і сама ознака.

Кожна середня величина характеризує досліджувану сукупність за якоюсь однією ознакою. Щоб отримати повне і всебічне уявлення про сукупність, що вивчається, по ряду істотних ознак, необхідно розташовувати системою середніх величин, які можуть описати явище з різних сторін.

Існують різні види середніх:

середня арифметична;

середня гармонійна;

середня геометрична;

середня квадратична;

середня кубічна.

Середні перелічених вище видів, своєю чергою, діляться на прості (невиважені) і зважені.

Розглянемо види середніх, які у статистиці.

Середня арифметична проста (невиважена) дорівнює сумі окремих значень ознаки, поділеної на число цих значень.

Окремі значення ознаки називають варіантами та позначають через х i (
); число одиниць сукупності позначають через n, середнє значення ознаки через . Отже, середня арифметична проста дорівнює:

або

приклад 1.Таблиця 1

Дані про виробництво робітниками продукції А за зміну

У цьому прикладі ознака, що варіює, - випуск виробів за зміну.

Чисельні значення ознаки (16, 17 і т. д.) називають варіантами. Визначимо середнє вироблення продукції робітниками цієї групи:

шт.

Проста середня арифметична застосовується у разі, коли є окремі значення ознаки, тобто. дані не згруповані. Якщо дані представлені у вигляді рядів розподілу чи угруповань, то середня обчислюється інакше.

Середня арифметична зважена

Середня арифметична зважена дорівнює сумі творів кожного окремого значення ознаки (варіанту) на відповідну частоту, поділену на суму всіх частот.

Число однакових значень ознаки в рядах розподілу називається частотою або вагою і позначається через f i.

Відповідно, середня арифметична зважена виглядає так:

або

З формули видно, що середня залежить лише від значень ознаки, а й їх частот, тобто. від складу сукупності, з її структури.

приклад 2.Таблиця 2

Дані про заробітну плату робітників

За даними дискретного ряду розподілу видно, що одні й самі значення ознаки (варіанти) повторюються кілька разів. Так, варіанти х 1 зустрічається в сукупності 2 рази, а варіанти х 2 - 6 разів і т.д.

Обчислимо середню заробітну плату одного робітника:

Фонд заробітної плати з кожної групи робочих дорівнює добутку варіанти на частоту (
), а сума цих творів дає загальний фонд заробітної плати всіх робітників (
).

Якби розрахунок був виконаний за формулою простої середньої арифметичної, середній заробіток дорівнював 3 000 руб. (). Порівнюючи отриманий результат з вихідними даними, очевидно, що середня заробітна плата має бути істотно вищою (більше половини робітників отримують заробітну плату вище 3000 руб.). Тому розрахунок за простою середньою арифметичною в таких випадках буде помилковим.

Статистичний матеріал у результаті обробки може бути представлений у вигляді дискретних рядів розподілу, а й у вигляді інтервальних варіаційних рядів із закритими чи відкритими інтервалами.

Розглянемо розрахунок середньої арифметичної для таких рядів.

Середнє значення це:

Середнє значення

Середнє значення- Чисельна характеристика безлічі чисел або функцій; - деяке число, укладене між найменшим та найбільшим із їх значень.

1 Основні відомості
2 Ієрархія середніх значень у математиці
3 У теорії ймовірностей та статистики
4 Див.
5 Примітки

Основні відомості

Вихідним пунктом становлення теорії середніх величин стало дослідження пропорцій школою Піфагора. При цьому не проводилося суворої різниці між поняттями середньої величини та пропорції. Значний поштовх розвитку теорії пропорцій з арифметичної точки зору було надано грецькими математиками - Нікомахом Гераським (кінець I - початок II ст. н. е.) і Паппом Олександрійським (III ст. н. е.). Першим етапом розвитку поняття середньої є етап, коли середня стала вважатися центральним членом безперервної пропорції. Але поняття середньої як центрального значення прогресії не дає можливості вивести поняття середньої по відношенню до послідовності n членів, незалежно від того, в якому порядку вони йдуть один за одним. Для цієї мети необхідно вдатися до формального узагальнення середніх. Наступний етап – перехід від безперервних пропорцій до прогресій – арифметичної, геометричної та гармонійної.

У історії статистики вперше широке вживання середніх величин пов'язані з ім'ям англійського вченого У. Петті. У. Петті одне із перших намагався надати середній величині статистичний сенс, пов'язавши її з економічними категоріями. Але опис поняття середньої величини, його виділення Петті не зробив. Родоначальником теорії середніх величин заведено вважати А. Кетле. Він одним із перших почав послідовно розробляти теорію середніх величин, намагаючись підвести під неї математичну базу. А. Кетле виділяв два види середніх величин - власне середні та середні арифметичні. Власне, середні представляють річ, число, що дійсно існують. Власне, середні або середні статистичні повинні виводитися з явищ одноякісних, однакових за своїм внутрішнім значенням. Середні арифметичні - числа, що дають можливо близьке уявлення про багато чисел, різних, хоча і однорідних.

Кожен із видів середньої може виступати або у формі простої, або у формі виваженої середньої. Правильність вибору форми середньої випливає із матеріальної природи об'єкта дослідження. Формули простих середніх застосовуються у разі, якщо індивідуальні значення ознаки, що усереднюється, не повторюються. Коли в практичних дослідженнях окремі значення ознаки, що вивчається, зустрічаються кілька разів у одиниць досліджуваної сукупності, тоді частота повторень індивідуальних значень ознаки присутня в розрахункових формулах статечних середніх. І тут вони називаються формулами зважених середніх.

Wikimedia Foundation. 2010 року.