Построение икосаэдра. Как сделать из бумаги икосаэдр? Руководство по выполнению

Рассмотрим алгоритмы построения геометрических моделей наиболее распространенных тел, которые часто используются как базовые элементы при построении более сложных моделей.

4.4.1. Построение правильных многогранников

Правильными многогранниками (платоновыми телами) называются такие выпуклые многогранники, все грани которых являются правильными многоугольниками и все многогранные углы при вершинах равны между собой.

Существует ровно 5 правильных многогранников: правильный тетраэдр, гексаэдр(куб), октаэдр, додекаэдр и икосаэдр. Их основные характеристики приведены в следующей таб. 4.2.

Правильные многогранники и их свойства				Таблица 4.2
Правильные многогранники и их свойства

Название
многогранника
Тетраэдр
Гексаэдр

Додекаэдр
Икосаэдр

Грани, ребра и вершины связаны между собой равенством Эй-

Г + В = Р + 2.

Для полного описания правильного многогранника вследствие его выпуклости достаточно указать способ отыскания всех его вершин. Куб (гексаэдр) построить совсем просто. Покажем, каким образом строятся остальные тела.

Для построения тетраэдра предварительно строится куб, на его противоположных гранях проводятся скрещивающиеся диагонали. Таким образом, вершинами тетраэдра являются любые 4 вершины куба, попарно не смежные ни с одним из его ребер рис.4.1.

тетраэдр

Рис. 4.1. Построение куба, тетраэдра и октаэдра

Для построения октаэдра предварительно строится куб. Вершины октаэдра – центры тяжести граней куба (рис.4.1), значит, каждая вершина октаэдра является средним арифметическим одноименных координат четырех вершин, образующих ее грань куба.

4.4.2. Построение икосаэдра

Икосаэдр и додекаэдр можно также построить при помощи куба. Однако существует и более простой способ конструирования:

- строятся две окружности единичного радиуса на расстоянии h=1;

- каждая из окружностей разбивается на 5 равных частей, как показано на рис. 4.2.











Рис. 4.2. Построение икосаэдра

- перемещаясь вдоль окружностей против часовой стрелки, нумеруем выделенные 10 точек в порядке возрастания угла поворота и затем последовательно в соответствии с нумерацией соединим эти точки прямолинейными отрезками;

- затем, стягивая хордами точки, выделенные на каждой из окружностей, получаем в результате пояс из 10 правильных треугольников;

- для завершения построения икосаэдра выберем на оси Z две точки так, чтобы длина боковых ребер пятиугольных пирамид с вершинами в этих точках и основаниями, совпадающими с построенными пятиугольниками, была равна длинам сторон пояса из треугольников. Нетрудно видеть, что для этого нуж-

ны точки с аппликатами ± 5 2 .

В результате описанных построений получаем 12 точек. Выпуклый многогранник с вершинами в этих точках будет иметь 20 граней, каждая из которых является правильным треугольником, и все его

многогранные углы при вершинах будут равны между собой. Тем самым результат описанного построения – икосаэдр.

4.4.3. Построение додекаэдра и сферы

Для построения додекаэдра воспользуемся свойством двойственности: вершины додекаэдра –центры (тяжести) треугольных граней икосаэдра. Значит, координаты каждой вершины додекаэдра можно найти, вычислив средние арифметические соответствующих координат вершин граней икосаэдра.

Для построения модели сферы используем построенный ранее икосаэдр. Заметим, что икосаэдр уже является моделью сферы: все вершины лежат на ее поверхности, все грани – равносторонние треугольники. Единственный его недостаток – это малое количество треугольных граней для передачи гладкой поверхности сферы. Для повышения уровня детализации модели используется следующая рекурсивная процедура:

каждая треугольная грань разбивается на четыре части, новые вершины берутся на серединах сторон грани, как показано на рис.4.3.;

Рис. 4.3. Грань икосаэдра

новые вершины проецируются на поверхность сферы, для этого из центра сферы через вершину проводится луч и вершина переносится в точку пересечения луча с поверхностью сферы;

указанные этапы повторяются до тех пор, пока не будет получена требуемая степень детализации поверхности сферы.

Рассмотренные алгоритмы позволяют получить параметры основных геометрических моделей. Аналогичным образом можно построить модели цилиндра, тора и других тел.

4.5. Полиномиальные параметрические формы представления

Полигональные модели обладают одним существенным недостатком: для получения реалистичной модели тел, имеющих сложную форму, требуются десятки тысяч полигонов. Реалистичные сцены насчитывают уже сотни тысяч полигонов. Одним из способов получения качественных моделей при значительном снижении вычислений является использование полиномиальных параметрических форм, которые используют полигональную сетку только для получения опорных точек.

4.5.1. Формы представления кривых и поверхностей

Существуют три главных формы математического представления кривых и поверхностей: явная, неявная, параметрическая.

Явная форма задания кривой в двухмерном пространстве представляет собой уравнение, в левой части которого стоит зависимая переменная, а в правой части – функция, аргументом которой является независимая переменная.

Неявная форма в двумерном пространстве f(x , y) =0. В параметрической форме в трехмерном пространстве:

уравнение кривой – x = x (u ), y = y (u ), z = z (u ) ;

уравнение поверхности – x = x (u , v ), y = y (u , v ), z = z (u , v ).

Одно из главных достоинств параметрической формы (ПФ) представления – ее единообразие в двух- и трехмерном пространствах. ПФ является, во-первых, наиболее гибкой, а во-вторых, устойчивой к любым вариациям формы и ориентации объектов, что делает ее особенно удобной в математическом обеспечении систем компьютерной графики.

Параметрические полиномиальные кривые и поверхности

Существует множество способов представления объектов, но мы сосредоточимся на полиномиальных, т.е. все функции параметра u при описании кривых или параметров u и v при описании поверхностей являются полиномами.

Рассмотрим уравнение кривой:

p (u ) = [ x (u ) y (u ) z (u )] T .

i = 0 j = 0

Полиномиальная параметрическая кривая степени n имеет вид (в OpenGL часто используется термин «порядок» полинома (order), который имеет значение на 1 больше, чем степень полинома)


p(u) = ∑ uk ck ,
k= 0

где c k имеет независимые компоненты x , y , z , т.е. c k = c xk		c zk

Матрица {c k }, состоящая из n +1 столбцов, объединяет коэффициенты полиномов для компонентов p ; это означает, что у нас есть 3(n +1) степеней свободы в выборе коэффициентов для конкретной кривой p .

Кривую можно определить на любом интервале изменения параметра u , но не теряя общности суждений, можно принять, что 0 ≤ u ≤ 1, т.о. определяется сегмент кривой.

Параметрическая полиномиальная поверхность описывается уравнением следующего вида:

x(u, v)

p(u, v) = y(u, v) = ∑∑ n m cij ui v j .

z(u, v)

Таким образом, для определения конкретной поверхности p (u ,v ) необходимо задать 3(n +1)(m +1) коэффициентов. Можно при анализе принять n=m , а параметры u и v изменять на интервале 0 ≤ u, v ≤ 1 и определить порцию поверхности (surface patch), показанной на рис. 4.4.

Рис. 4.4. Определение порции поверхности

Определенный таким способом участок поверхности можно рассматривать как предел, к которому стремится множество кривых, которые формируются, когда один из параметров u или v пробегает значения в своем интервале, в то время как другой сохраняет посто-

янное значение. В дальнейшем вначале будем определять полиномиальные кривые, а затем применять их для формирования поверхности с аналогичными характеристиками.

Отметим преимущества использования полиномиальной параметрической формы представления:

возможность локального контроля формы объекта;

гладкость и непрерывность в математическом смысле;

возможность аналитического вычисления производных;

устойчивость к малым возмущениям;

возможность использовать относительно простые, а значит, высокоскоростные методы тонирования.

4.5.2. Параметрически заданные кубические кривые

Если воспользоваться полиномом очень высокой степени, будет больше «свободы», но потребуется и больше вычислений при расчете координат точек. Также при росте степени свободы возрастает опасность получить волнистую форму кривой. С другой стороны, выбор полинома слишком низкой степени даст нам слишком мало параметров, и не удастся воспроизвести форму кривой. Решение – кривая разбивается на сегменты, которые описываются полиномами низкой степени.

Описать кубическую полиномиальную кривую можно следующим образом:

p(u) = c0 + c1 u + c2 u2 + c3 u3 = ∑ uk ck = uT c,

		k= 0

где c = [ c 0 c 1 c 2c 3 ] ,	u = 1 u u	c k = c xk	c yk c zk

В этих выражениях c представляет собой матрицу коэффициентов полинома. Именно ее и требуется вычислять по заданному ансамблю опорных точек. Далее рассмотрим разные классы кубических кривых, которые отличаются характером сопоставления с опорными точками. Для каждого типа будет сформирована система из 12 уравнений с 12-ю неизвестными, но, поскольку параметрические функции для компонентов x,y,z независимы, эти 12 уравнений будет разделены на три группы по 4 уравнения с 4-мя неизвестными.

Вычисление значений коэффициентов определенного типа кубической кривой выполняется по заданному ансамблю опорных точек, соответствующих некоторым значениям независимого параметра

u . Эти данные могут иметь форму ограничений, требующих, чтобы кривая проходила через некоторые из заданных точек и в окрестности других точек. Кроме того, эти данные накладывают и определенные условия на гладкость кривой, например непрерывность производных в заданных точках сопряжения отдельных сегментов. Кривые разного класса, сформированные на одних опорных точках, могут существенно отличаться.

4.5.3. Интерполяция

Пусть имеются четыре опорные точки в трехмерном пространстве: p 0 , p 1 , p 2 и p 3 . Каждая точка представлена тройкой своих координат:

p k = [ x k y k z k ] T .

Найдем элементы матрицы коэффициентов c , такие, что полином p(u)=u T c будет проходить через заданные четыре опорные точки.

Решение. Есть четыре точки, составляем 12 уравнений с 12-ю неизвестными – элементами матрицы c . Полагаем, что значения u k (k= 0,1,2,3) распределены равномерно на интервале , т.е. u= 0,1/3,2/3,1. Получаем уравнения:

P (0) = c 0 ,

c 3 ,

p 3 = p (1 ) = c 0 + c 1 + c 2 + c 3 .

Запишем эти уравнения в матричной форме: p=AC ,

p = [ p 0 p 1 p 2 p 3 ] T






			(2 3 )				(2 3 )

Проанализируем матрицу A . Если интерпретировать p и c как матрицы-столбцы из 12 элементов, то правило умножения матриц соблюдено не будет. Но мы можем рассматривать p и c как матрицы столбцы из 4-х элементов, каждый из которых в свою очередь является матрицей-строкой. Тогда в результате произведения получим элемент того же вида, что и элементы матрицы столбца p . Матрица не является вырожденной, ее можно обратить и получить базисную ин-

терполяционную матрицу:



M I = A − 1 = − 5.5		− 4.5
	− 22.5		− 4.5
		− 13.5
− 4.5		− 13.5

Располагая значениями M I , можно вычислить искомые значения коэффициентов c= M I /p .

Если кривая задана не 4-мя, а m опорными точками, то можно представить интерполяционным полиномом (m -1)-го порядка (рассчитать 3× m коэффициентов, используя аналогичную методику). Можно поступить иначе – считать эту кривую состоящей из нескольких сегментов, каждый из которых задается очередной группой из 4-х точек. Непрерывность можно обеспечить тем, что считать последнюю опорную точку предшествующей группы первой опорной точкой следующей группы. Матрицы M I на каждом сегменте будут одинаковы, т.к. u . Но в этом случае функции производных по па-

раметру будут претерпевать разрыв в точках сопряжения.

4.5.4. Функции смешивания (полиномиальные весовые функции опорных точек)

Проведем анализ гладкости интерполяционных полиномиальных кривых. Для этого перепишем выведенные ранее соотношения в слегка измененном виде:

p(u) = uT с = uT M I p .

Это соотношение можно записать в виде: p (u ) = b (u ) T p ,

b(u) = M I T u ,

есть матрица-столбец из четырех полиномиальных функций смеши-

вания (blending polynomials) :

b (u ) = [ b 0 (u ) b 1 (u ) b 2 (u ) b 3 (u )] T .

В каждой функции смешивания полином является кубическим. Выразив p (u ) как сумму полиномов смешивания, получим:

p (u ) = b 0 (u ) p 0 + b 1 (u ) p 1 + b 2 (u ) p 2 + b 3 (u ) p 3 = ∑ b i (u ) p i .

i= 0

Из этого соотношения следует, что полиномиальные функции смешивания характеризуют вклад, который вносит каждая опорная точка, и таким образом позволяют оценить, насколько скажется на виде конечной кривой изменение положения той или иной опорной точки. Аналитические выражения для них:

b 0 (u ) = − 9 2 (u − 1 3 )(u − 2 3 )(u − 1), b 1 (u ) = 27 2 u (u − 2 3 )(u − 1),

b 2 (u ) = − 27 2 u (u − 1 3 )(u − 1), b 3 (u ) = 9 2 (u − 1 3 )(u − 2 3 ) .

Т.к. все нули функций лежат на отрезке , то их значения могут существенно изменятся на этом интервале, а сами функции не являются монотонными (рис. 4.5.). Эти характеристики следуют из того, что интерполяционная кривая должна проходить через опорные точки, а не в ближайшей их окрестности. Плохая гладкость кривой, отсутствие непрерывности производных в точках стыка сегментов объясняют, почему интерполяционные полиномиальные кривые редко используются в КГ. Но пользуясь той же методикой анализа, можно отыскать более подходящий тип кривой.


		b1 (u)	b2 (u)

				b3 (u)
				b3 (u)



Рис. 4.5. Полиномиальная функция смешивания
	для случая кубической интерполяции

Порция кубической интерполяционной поверхности

Бикубическое уравнение поверхности можно записать следующим образом:

p(u, v) = ∑∑ ui v j cij .

i = 0 j = 0

Здесь c ij – трехкомпонентная матрица-столбец, элементами которой являются коэффициенты при одинаковых степенях независимой переменной в уравнениях для x , y , z- компонент. Определим матрицу C 4x4 таким образом, что ее элементами будут трехкомпонентные мат- рицы-столбцы:

C = [ cij ].

Тогда описать порцию поверхности можно следующим образом: p (u , v ) = u T Cv ,


v = 1 v v

Конкретная порция бикубической поверхности определяется 48 значениями элементов матрицы C – 16-ю трехмерными векторами.

Допустим, что имеется 16 трехмерных опорных точек p ij , i= 0,..,3, j= 0,..,3 (рис. 4.6.). Будем считать, что эти данные используются для интерполирования с равным шагом по обоим независимым параметрам u и v , которые принимают значения 0, 1/3, 2/3, 1. Отсюда

получим три набора из 16 уравнений с 16 неизвестными в каждом. Так, при u=v= 0 получим

p 00 = [ 1 0 0 0] C 0 0 = c 00 .0

Рис. 4.6. Порция интерполяционной поверхности

Можно не решать все эти уравнения. Если зафиксировать v =0, то, изменяя u , получим кривую, проходящую через p 00 , p 10 , p 20 , p 30 . Используя результаты, полученные в предыдущем разделе, можем записать для этой кривой следующее соотношение:


p (u ,0) = u T M
p (u ,0) = u T M				UT C .

При значениях v= 1/3, 2/3, 1 можно определить три другие интерполяционные кривые, каждую из которых можно описать тем же способом. Объединив уравнения для всех кривых, получим интересующую нас систему из 16 уравнений:

uT M I P = uT CAT ,

где A – матрица, обратная M I . Решением этого уравнения будет искомая матрица коэффициентов:

C = M I PM I T .

Подставляя ее в уравнение поверхности, окончательно получим p (u ,v ) = u T M I PM I T v .

Этот результат можно интерпретировать по-разному. Из него следует, во-первых, что результаты, полученные при анализе кривых, можно распространить на соответствующие поверхности. Во-вторых, можно распространить на поверхности методику использования полиномиальных функций смешивания:

p(u, v) = ∑∑ bi (u) bj (v ) pij .

i = 0 j = 0

4.5.5. Форма представления кривых и поверхностей Эрмита

Пусть имеются точки p 0 , p 3 и сегменту соответствует интервал u , т.е. имеющиеся точки соответствуют u =0 и u =1. Запишем

два условия:

p (0) = p 0 = c 0,

p (1) = p 3 = c 0 + c 1 + c 2 + c 3.

Два других условия получим, задав значения производных функций в крайних точках сегмента u =0 и u =1:

p " (u ) = c 1 + 2uc 2 + 3u 2 c 3 , тогда

p " 0 = p " (0) = c 1 ,

p " 3 = p " (1) = c 1 + 2 c 2 + 3 c 3.

Запишем эти уравнения в матричной форме:






p " 3
Обозначив через q вектор данных
q = [ p0	p " 0	p " 3 ] T ,

можно записать уравнение в виде:

c = M H q ,

где MH называется обобщенной матрицей Эрмита (Hernite geometry matrix).





−3		−2	−1
	−2
	−2

В результате получим представления полиномиальной кривой в форме Эрмита:

p(u) = uT M H q.

Будем использовать форму Эрмита для представления сегментов составной кривой, как показано на рис. 4.7. Точка сопряжения является общей для обоих сегментов, и, кроме того, производные к кривой в точке сопряжения для обоих сегментов также равны. В результате получаем составную кривую, непрерывную по первой производной на всем протяжении.

p(0) p(1)=q(0)

Рис. 4.7. Применение формы Эрмита к стыковке сегментов

Возможность получения более гладких кривых при использования формы представления по Эрмиту можно обосновать математически следующим образом. Запишем полином в виде

p(u) = b(u) T q,

где новая функция смешивания имеет вид



b(u) = M T u =	− 2 u 3 + 3 u 2 .
		−2 u 2 +u
		u 3 − u 2
		u 3 − u 2

Нули четырех этих полиномов расположены вне интервала , а потому функции смешивания являются гораздо более гладкими, чем для интерполяционных полиномов.

Можно следующим образом определить порцию поверхности в форме Эрмита:

p (u , v ) = ∑∑ b i (u ) b j (v) q ij ,

i = 0 j = 0

где Q =[ q ij ] – набор данных, представляющих порцию поверхности аналогично тому, как q представляет сегмент кривой. Четыре элемента Q представляют собой значения функции p (u,v ) в угловых точках поверхности, а четыре других должны представлять производные к поверхности в этих угловых точках. В интерактивных приложениях пользователю желательно специфицировать не данные о производных, а координаты точек, и, следовательно, не сформулировав аналитические выражения для этих данных, мы не сможем получить производные.

Если в точке сопряжения значения всех трех параметрических компонент векторов p и q равны, то имеет место параметрическая непрерывность (parametric continuity) класса С 0 .

Кривые, в которых условия непрерывности удовлетворяются и для значения, и для первой производной, обладают параметрической непрерывностью класса С 1 .

Если значения компонент производных пропорциональны, то имеет место геометрическая непрерывность класса G 1 .

Эти идеи можно обобщить для производных более высоких порядков.

Форма кривой, обладающей геометрической непрерывностью класса G 1 , зависит от коэффициента пропорциональности длин касательных к сегментам в точке сопряжения. На рис.4.8. показано, что форма сегментов кривых, совпадающих в конечных точках и имеющих в этих точках пропорциональные векторы касательных, довольно существенно отличается. Это свойство часто используется в графических программах вычерчивания.

p"(0) q(u) p"(1)

Рис. 4.8. Влияние длины вектора касательных на форму сегментов

4.5.6. Кривые и поверхности в форме Безье

Сравнение кривых в форме Эрмита и в форме интерполяционного полинома невозможно, т.к. для их формирования используются

разные по характеру наборы данных. Попробуем использовать один и тот же ансамбль опорных точек и для определения интерполяционного многочлена и для косвенного задания кривых в форме Эрмита. В результате этого получим кривую в форме Безье (Bezier), которая является хорошим приближением кривой в форме Эрмита и которую можно сравнивать с интерполяционным полиномом, сформированным на том же ансамбле точек. Кроме того, такая процедура идеально подходит для интерактивного построения криволинейных объектов в системах КГ и САПР, т.к. определение кривой в форме Безье не требует задания производных.

Кривые Безье

Пусть имеются четыре опорные точки в трехмерном пространстве: p 0 , p 1 , p 2 и p 3 . Конечные точки формируемой кривой p (u ) должны совпадать с опорными точками p 0 , p 1 :

p 0 = p (0), p 3 = p (1) .

Безье предложил использовать две другие опорные точки p 1 и p 2 для задания производных в крайних точках сегмента u= 0 и u= 1. Вос-

пользуемся для этого линейной аппроксимацией (рис.4.9).
p "(0) =	p 1 − p 0	3(p − p ),	p "(1) =	p 3 − p 2	3(p − p
p "(0) =		3(p − p ),	p "(1) =		3(p − p

Рис. 4.9. Аппроксимация векторов касательных

Применив эту аппроксимацию к касательным в двух крайних точках к параметрической полиномиальной кривой p (u ) = u T c , получим два условия:

3 p 1 − 3 p 0 = c 1,

3 p 3 − 3 p 2 = c 1 + 2 c 2 + 3 c 3.

Добавим их к уже имеющимся условиям совпадения кривой в конечных точках:

p (0) = p 0 = c 0 ,

p (1) = p 3 = c 0 + c 1 +c 2 + c 3 .

Итак, мы снова получили три набора по четыре уравнения относительно четырех неизвестных в каждом. Решая их по той же методике, что и в предыдущем разделе, получим:

c = M B p ,

где M B называется базисной матрицей Безье (Bezier geometry matrix):



= − 3
		−6
	−1		−3
	−1		−3

В результате получим представления полиномиальной кривой в форме Безье:

p(u) = uT M B p .

Эту формулу можно использовать для получения составной кривой, сегменты которой являются интерполяционными полиномами. Очевидно, что составная кривая, построенная по методу Безье на произвольном ансамбле опорных точек, относится к классу С 0 , но требованиям класса С 1 она не удовлетворяет, т.к. касательные справа и слева от точки сопряжения аппроксимируются по разным формулам.

Проанализируем свойства кривой с помощью функций смешивания. Запишем полином в форме:

p(u) = b(u) T p,

где новая функция смешивания имеет вид (рис. 4.10):

		−u )
		−u )
b(u) = M T u = 3 u (1 − u ) 2
	3u 2	(1− u )

Эти четыре полинома являются частными случаями полиномов Бернштейна :

b kd (u ) = k !(d d − ! k )! u k (1− u )d − k .

Свойства полиномов Бернштейна:

1) все нули в точках u= 0 или u= 1;

2) p (u ) должна лежать внутри выпуклой многоугольной оболочки, образованной четырьмя заданными точками, как показано на рис. 4.11. Таким образом, хотя кривая Безье и не проходит через все заданные опорные точки, она никогда не выходит за пределы области, ограниченной этими точками. Это очень удобно при интерактивном визуальном конструировании.






		Рис. 4.11. Выпуклая оболочка и
Рис. 4.10. Полиномиальные функции		Рис. 4.11. Выпуклая оболочка и

Порции поверхности в форме Безье

Порции поверхностей Безье можно сформировать с помощью функций смешивания. Если P = [ p ij ] – массив опорных точек с раз-

мерами 4x4, то соответствующая порция поверхности в форме Безье описывается соотношением:


p(u, v) = ∑∑ bi ( u) bj (v ) pij = uT M B PM B T v.
i= 0	j= 0

Порция поверхности проходит через угловые точки p 00 , p 03 , p 30 и p 33 и не выходит за пределы выпуклого многоугольника, вершинами которого являются опорные точки. Двенадцать опорных точек из 16

можно интерпретировать как данные, определяющие направление производных по разным параметрам в угловых точках формируемой порции поверхности.

4.6. Пример построения полигональных моделей

Рассматриваемую задачу – представление геометрических моделей, задаваемых полигональным сетками, – можно разбить на следующие этапы:

1) разработка модели (структур данных) для представления сцены;

2) разработка формата файла, для хранения модели;

3) написание программы для просмотра созданных сцен;

4) написание программы для генерации полигональных моделей объектов в соответствии с вариантом задания.

4.6.1. Разработка структур данных полигональной модели

Можно выделить следующие элементы модели: точка, полигон, модель отдельного объекта, сцена (множество объектов с заданным расположением относительно друг друга).

1) Точка описывается тремя координатами:

2) Полигон – в общем случае произвольный выпуклый многоугольник. Мы будем использовать его частный случай – треугольник. Наш выбор обоснован тем, что последующие алгоритмы закраски с Z-буфером, для своей работы будут требовать именно треугольные

грани и все более сложные многоугольники потребуется разбивать.

typedef struct Polygon {

int Points; //индексы трех вершин, образующих //полигон, вершины хранятся в списке вершин модели

3) Модель отдельного объекта представляет собой список точек и список вершин:

typedef struct Model3D {

Polygon Polygons; //массив полиго-

4) Сцена – это множество объектов с заданным расположением относительно друг друга. В простейшем случае можно использовать

список (массив) объектов, например,

4.6.2. Разработка формата файла для хранения модели

Для хранения и обработки сцен и моделей удобно использовать текстовые файлы, состоящие из различных секций. Секции могут разделяться ключевыми словами, которые делают чтение и редактирование файлов более простым, а также дают возможность задания для модели только части информации. Хорошим примером является формат DXF, который используется для обмена чертежей между САПР-системами. Рассмотрим простой пример:

где первое число – количество моделей в файле сцены N. Далее следует N моделей. Первым числом в описании моделей является количество вершин K. Далее последовательно перечисляются координаты

x,y,z всех К вершин. После этого идет число G, задающее количество граней в модели. После чего следует G строк, каждая из которых содержит индексы трех вершин, образующих треугольную грань.

4.6.3. Просмотр созданных сцен

Для просмотра созданных сцен в ортографической проекции разработана следующая программа:

#include #include #include #include

const int MAX_MODEL_COUNT = 3; //макс. к-во моделей в сцене const int MAX_POINT_COUNT =100; //макс. к-во точек в модели const int MAX_POLY_COUNT =100; //макс. к-во граней в модели

typedef struct Point { double x, y, z;

typedef struct Polygon {

int Points; //индексы трех вершин, образующих полигон

typedef struct Model3D {

int PolygonCount;//количество полигонов в модели

Polygon Polygons; //массив полигонов

Model3D Models; //массив моделей

//функция выполняет чтение сцены из файла

void LoadScene(Scene3D &scene, const char * filename)

if ((f = fopen(filename, "rt")) == NULL)

fprintf(stderr, "Cannot open input file.\n"); exit(1);

//читаем к-во моделей в файле fscanf(f, "%d", &scene.ModelsCount);

for(int m = 0; m < scene.ModelsCount; ++m)

Model3D *model = &scene.Models[m]; //загрузка списка точек модели fscanf(f, "%d", &model->PointCount);

for(int i = 0; i < model->PointCount; ++i)

fscanf(f, "%lf%lf%lf", &p.x, &p.y, &p.z); model->Points[i] = p;

Polygon *p = &(model->Polygons[i]); fscanf(f, "%d%d%d", &(p->Points),

&(p->Points), &p->Points);

//вывод на экран каркасной //модели в ортографической проекции

//недостаток - все ребра рисуются по два раза void DrawWireFrameScene(const Scene3D &scene)

for(int m = 0; m < scene.ModelsCount; ++m)

const Model3D *model = &scene.Models[m]; for(int i = 0; i < model->PolygonCount; ++i)

const Polygon *poly = &model->Polygons[i];


			&model->Points;
			&model->Points;
			&model->Points;
line(320 + p1->x,

line(320 + p2->x,

line(320 + p3->x,

//инициализация графического режима void InitGraphMode(void)

int gdriver = DETECT, gmode, errorcode; initgraph(&gdriver, &gmode, "");

errorcode = graphresult();

if (errorcode != grOk) //an error occurred

printf("Graphics error: %s\n", grapherrormsg(errorcode));

printf("Press any key to halt:");

	//возвращаем код ошибки
	//возвращаем код ошибки

Scene3D scene; LoadScene(scene, "model.dat"); InitGraphMode(); DrawWireFrameScene(scene); getch();

Приведенный пример позволяет загружать сцены, заданные в описанном формате, и отображать их в ортографической проекции. Он демонстрирует базовые принципы работы с полигональными моделями.

Но из-за упрощения для повышения наглядности он имеет следующие существенные недостатки:

1) количество вершин, граней, моделей задается непосредственно в программе, а должна использоваться динамическая память, например динамический одномерный массив, память под который будет выделяться при загрузке сцены.

2) если имеется несколько одинаковых моделей, отличающихся только положением и ориентацией в пространстве, то данные описывающие их геометрию, дублируются, например несколько моделей сфер. Целесообразно разделить модель на две составляющие: геометрическую, хранящую описание граней, вершин, и топологическую, т.е. конкретный экземпляр объекта, расположенный в пространстве.

3) описание структур данных и методы, их поддерживающие, следует выделить в отдельный модуль, тогда его можно будет использовать, например, в программах генерации примити-

Таким образом, в настоящее время доминируют полигональные геометрические модели. Это вызвано простотой программного и аппаратного их представления. В виду постоянного роста возможностей

вычислительной техники с одной стороны и требований к качеству моделей с другой ведутся интенсивные исследования новых типов моделей.

Контрольные вопросы и упражнения

1. Чем отличаются геометрические модели от других видов моделей?

2. Назовите основные компоненты геометрической модели.

3. Чем отличаются координатные модели от аналитических?

4. Какие виды геометрических моделей существуют?

5. Почему полигональные модели получили широкоераспространение?

6. Какие способы задания полигональной модели вы знаете?

7. Какие недостатки и ограничения имеют полигональные модели?

8. Реализуйте алгоритмы построения полигональных моделей додекаэдров, икосаэдров и сфер.

9. Предложите алгоритм построения полигональной модели тора.

10. Каким образом можно сократить объем данных, хранимых

в памяти ЭВМ, при многократном использовании одинаковых полигональных моделей?

У многих конструкторов вырабатывается привычка мысленно изменять предметы и конструкции, попадающие им в руки или на глаза, в поисках более рационального решения или просто из любопытства: а что из этого выйдет? Приведенный ниже пример иллюстрирует такого рода упражнения-развлечения конструктора.

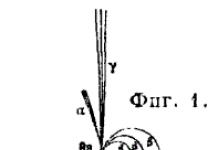
На рисунке 1 сплошными линиями показана развертка, состоящая из двадцати одинаковых равносторонних треугольников.

Если начертить развертку на плотной бумаге, вырезать ее, надрезать бумагу не очень острым ножом по линиям, отделяющим треугольники друг от друга и от лапок, согнуть развертку по этим линиям в одну сторону, склеить друг с другом концы полоски, состоящей из треугольников 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, а из треугольников 1, 5, 9, 13, 17 и 3, 7, 11, 15, 19 склеить две пятигранные пирамидки, то вы будете полностью вознаграждены за свой труд. В ваших руках окажется тело, замечательное по совершенству формы,- правильный двадцатигранник (икосаэдр), имеющий двадцать одинаковых граней - равносторонних треугольников, тридцать одинаковых ребер и двенадцать выступов, состоящих из пятигранных пирамидок. Неожиданно вместо двух склеенных пирамидок их оказалось шесть пар с шестью осями, проходящими через эти пары. Икосаэдр симметричен относительно всех шести осей. Вершина каждой из двенадцати пирамидок и три угла каждой грани касаются шаровой поверхности. Остальные точки граней близки к ней. По сравнению с гранями других правильных многогранников грани икосаэдра ближе всего расположены к поверхности описанной сферы, число граней максимально, и форма его ближе всего к форме шара. Отсюда возникает возможность строить, например, карту планеты на двадцати равносторонних треугольниках, проектируя точки сферы с помощью ее радиусов на грани вписанного икосаэдра. Возможность применения этого способа может быть выяснена более глубоким анализом.

Теперь представим себе, что икосаэдр является не оболочкой, а сплошным телом. Мысленно будем изменять его форму, постепенно и равномерно срезая верхушки всех пирамидок плоскостями, перпендикулярными к их осям. Появится двенадцать новых граней в виде правильных пятиугольников, а у бывших треугольных граней срежутся уголки, они превратятся в шестиугольники с тремя новыми небольшими сторонами вместо срезанных углов. При дальнейшем срезании пирамидок пятигранники увеличиваются, а у шестигранников короткие стороны растут, длинные сокращаются и, наконец, получается новая интересная форма многогранника, состоящего из двенадцати равносторонних пятиугольников и двадцати равносторонних шестиугольников. С такой выкройки делают футбольные мячи.

Если срезать пирамидки дальше, то площадь пятиугольников продолжает возрастать, а шестиугольники становятся неравносторонними, прежние их стороны станут короче новых, и так будет продолжаться до тех пор, пока прежние стороны не исчезнут, а новые сомкнутся в треугольники. Получим новую интересную форму многогранника, состоящую из двенадцати правильных пятиугольников и двадцати равносторонних треугольников. При дальнейшем срезании материала с плоскости пятигранников они превратятся в десятигранники, а треугольники уменьшатся в своих размерах. Наступит момент, когда неравные стороны десятигранников сравняются и получится новая форма - двенадцать равносторонних десятиугольников и двадцать маленьких равносторонних треугольников. Продолжая снимать материал с плоскостей десятиугольников, в конце концов снова получим двенадцать равносторонних пятиугольников, а треугольники исчезнут. Это будет известная форма двенадцатигранника пентагон-доде-каэдра. Из таких двенадцати пластинок, но выдавленных по сфере, был изготовлен советский вымпел, посланный на Луну. На рисунке дана его развертка (рис. 2).

При срезании двадцати трехгранных углов получим вместо них двадцать треугольников, пятиугольные грани превратятся в десятиугольные. Если продолжать эту операцию дальше, получим те же самые формы, что и при срезании углов у икосаэдра, но в обратном порядке и в конце концов опять получим икосаэдр, но значительно меньших размеров.

Практическая применимость рассмотренных здесь форм довольно ограниченна, они разве только могут быть использованы при огранке драгоценных камней.

Много интереснее исследовать икосаэдр не как сплошное тело, а как оболочку. В этом случае он представляет собой замкнутый объем, например, сосуд для жидкости и газа, изготовленный из плоского листа. Жесткость оболочке придают ребра. Ребра могут быть заменены стержнями или нитями, и тогда возникают другие вариации: жесткая корзинка или мягкая сетка с крупными ячейками.

Дальнейшие вариации будем производить с разверткой (рис. 1), видоизменение которой будет приводить иногда к неожиданным результатам.

Прибавим к развертке еще четыре треугольника, как показано пунктиром на рисунке 1. Шесть равносторонних треугольников с каждой стороны ленты согнутся теперь не в пирамидки, а уложатся в плоские правильные шестиугольники и на развертке могут быть ими заменены. После склейки получим барабан, состоящий из двенадцатигранной обечайки и двух шестиугольных донышек (рис. 3).

Аналогичный барабан можно получить из икосаэдра, если две противоположные пятигранные пирамидки заменить пятиугольными донышками.

Отрежем теперь от развертки треугольники 17-20. Из оставшихся треугольников 1-16 получим шестнадцатигранник с двумя четырехгранными пирамидками и одной продольной осью (рис. 4).

Если срезать четырехгранные пирамидки и заменить их квадратными гранями, получим десятигранник, состоящий из восьми треугольных и двух квадратных граней (рис. 5).

Отрежем теперь от развертки (рис. 1) еще четыре грани. Из оставшихся треугольников 1-12 неожиданно получается шестигранник, потому что каждая пара треугольников образовала одну грань в виде ромба (рис. 6).

Это ромбический додекаэдр, назовем его «ромбоидом», имеет, как и куб, шесть граней, восемь трехгранных углов и двенадцать ребер. Если его положить на одну из граней, то в нем нетрудно узнать перекошенный по диагонали куб. Если такой ромбоид сделать из двенадцати стержней вместо ребер, соединив их по углам шарнирно, то при растягивании его вдоль продольной оси стержни сложатся в палку, состоящую из трех стержней по концам и из шести посередине. При продольном сжатии этой палки стержни разойдутся сначала в вытянутый ромбоид, потом в куб, потом в сплющенный ромбоид и, наконец, уложатся в одну плоскость в виде правильного шестиугольника. Вот и идея для конструктора - табуретка и зонт, складывающиеся в виде палки.

Вариант ромбоида, сильно вытянутый вдоль своей оси (рис. 7, развертка 8), представляет особый интерес.

Такое тело с большим удлинением λ = 1/d (то есть с большим отношением длины 1 к толщине d), при полете ориентированное так, что ось направлена по полету, и двигающееся со скоростью, равной или большей скорости звука, вероятно, будет иметь наименьшее лобовое сопротивление по сравнению с другими телами такого же удлинения, потому что передние и задние ребра тела направлены по обтекающему потоку, а средние шесть ребер образуют с потоком очейь острые углы. Это утверждение требует еще доказательства или проверки экспериментом.

Срезая у ромбоида (рис. 6) обе трехгранные пирамидки (для чего все ромбы придется разрезать пополам), опять неожиданно получим хорошо известный правильный восьмигранник - октаэдр (рис. 9). Его развертка состоит из треугольников 1, 2, 4, 6, 8, 10, 11, 12. Между октаэдром и кубом существуют «родственные» отношения, аналогичные отношениям между икосаэдром и Пентагон-додекаэдром.

Срезая углы первого, получают второй через промежуточные четырнадцатигранники.

Из развертки, состоящей из треугольников 1, 2, 4, 5, 6, 7, 8, 10, 11, 12, склеивается правильный десятигранник, состоящий из двух пятигранных пирамид, сложенных основаниями. Из треугольников 2, 4, 6, 8, 10, 12 получаем развертку правильного шестигранника, представляющего собой два приложенных друг к другу тетраэдра, а развертка тетраэдра - правильного четырехгранника - состоит из треугольников 2, 4, 6, 8 (рис. 10).

Интересно отметить, что у тетраэдра четыре грани и четыре выступа, поэтому из тетраэдра, срезая трехгранные углы, получим опять тетраэдр через промежуточные восьмигранники с треугольными и шестиугольными гранями.

Наконец, из двух треугольников тоже можно склеить «тело», но это будет плоский треугольник, двусторонний, то есть тело, не имеющее объема.

Итак, оказывается, что правильные многогранники можно склеивать из четного числа равносторонних треугольников. При этом из двух получается «тело без объема». Из двенадцати треугольников получается ромбоид, то есть шестигранник с ромбическими гранями или тело без объема в виде двух склеенных правильных шестиугольников. Из двадцати четырех треугольников получаем четырнадцатигранник, у которого две грани- правильные шестиугольники. Попутно предлагается задача для читателей: можно ли склеить замкнутую фигуру другим способом из четырнадцати, восемнадцати и двадцати двух равносторонних треугольников?

Рассмотрим еще одну возможность варьирования развертки, показанной на рис. 1. Если отбросить верхние и нижние зубцы и оставить только ленту, состоящую из четных номеров треугольников, а затем сложить несколько таких лент их боковыми кромками, то получим развертку, показанную на рисунке 11.

Развертка дана для двенадцати треугольников в каждой ленте. Начертив и вырезав эту развертку, согните ее по косым линиям в одну сторону, а по горизонтальным - в другую. В склеенном виде получаем фигуру, близкую к круглому цилиндру, но с граненой боковой поверхностью. Эта фигура получается жесткой на кручение, на изгиб, на продольное сжатие и с местной жесткостью боковой стенки. Эта вариация, пожалуй, будет наиболее ценной б практическом применении. Она может служить схемой строительной конструкции, легкой, прочной, жесткой и сейсмостойкой. Она не слишком сложна в производстве и может быть осуществлена как в стеночном варианте, так и ферменном, если ребра заменить стержнями. Во втором случае, составленная из треугольников, она будет статически определимой.

(в биологии)

Многие люди любят создавать подделки из бумаги, причем это совсем не зависит от их возраста, такому занятию подвержены как дети, так и взрослые. Единственное отличие, состоит в том, что взрослые любят создавать более сложные фигуры. Особенно часто, почему-то, создаются геометрические фигуры. В нашей статье мы расскажем вам, как сделать из бумаги икосаэдр. Именно такое название получил сложный, правильный многоугольник, который имеет целых двадцать треугольных граней и тридцать ребер. Как вы могли отметить, такая фигура довольно-таки сложная на вид. Даже если вы новичок в оригами, то наш метод не покажется сложным и вы с легкостью его склеите из бумаги.

Среди всего многообразия материалов, которые используются для его изготовления, вы можете взять следующие: гофрированную бумагу, фольгу, бумагу для упаковки подарков или для цветов. С помощью различных других материалов, вы сможете улучшить вашу фигуру и украсить ее. Не ограничивайте в этом деле вашу фантазию, и она вам поможет.

Перед тем как начать, вам нужно подготовиться. Для этого вам могут пригодится следующие материалы:

Заготовка фигуры, которую нужно перенести на материал для нашей фигуры.
Клей. Лучше всего использовать ПВА - он сохнет достаточно долго, чтобы вы могли исправить ошибки при склеивании.
Ножницы.
Линейка.

Как только вы раздобудете все необходимые компоненты, то вы можете начинать работу. Теперь мы представим схему, по которой можно изготовить эту фигуру:

Итак, наша фигурка готова и теперь вы сможет заняться ее украшением. Его можно разрисовать красками или карандашами, подвесить на веревочке. Также прекрасно подойдут различные блестки, кусочки дождика. Очень часто, такое украшение можно использовать в качестве игрушки на новогоднюю елку. Кроме этого, вы можете сделать очень забавную вещь, используя икосаэдры, а именно - футбольный мяч, который является усеченной фигурой. Если внимательно его осмотреть, то вы заметите, что он состоит из двенадцати пятиугольников и двадцати шестиугольников, которые имеют одинаковые размеры. Разукрашенная фигурка будет прекрасно смотреться, а разные цвета простых элементов еще сильнее покажут такую разницу.

Если такая идея вас заинтриговала, то ниже мы представляем развертку, с помощью которой вы сможете сделать мяч:

Как видите, создание фигурок из бумаги - это очень интересный процесс. Когда вы научитесь делать икосаэдр, то можете переходить к другим, более сложным геометрическим фигурам. Особенно это полезно для детей, которые могут с ранних лет развивать пространственное мышление, изучать геометрию и улучшать мелкую моторику. Если ребенок совсем маленький, то может потребоваться помощь родителей, впрочем, с готовой игрушкой он будет радостно играться самостоятельно. Тем не менее взрослым такое занятие будет тоже полезно - это прекрасное хобби, которое может помочь расслабится в или просто скоротать время. Если вы любите не кропотливую и требующую внимания работу, то такое занятие как раз то что надо.

Мы надеемся, что наша статья о том, как сделать икосаэдр из бумаги, заинтересовала вас. Возможно именно с этой фигуры вы начнете заниматься поделками из бумаги. Удачи и успехов во всех начинаниях!

Видео уроки

Перед тем как начать, вам нужно подготовиться. Для этого вам могут пригодится следующие материалы:

Заготовка фигуры, которую нужно перенести на материал для нашей фигуры.
Клей. Лучше всего использовать ПВА - он сохнет достаточно долго, чтобы вы могли исправить ошибки при склеивании.
Ножницы.
Линейка.

Видео уроки

Создавать поделки своими руками интересно не только детям, но и взрослым. Однако для взрослых придумано достаточное количество моделей, которые отличаются сложностью выполнения и временем, затраченным на их создание. В последнее время у взрослых и детей появился интерес к созданию сложных геометрических фигур. К такому виду фигур относится икосаэдр, который представляет собой правильный многоугольник и является одним из платоновых тел – правильных многогранников. Эта фигура имеет 20 треугольных граней (равносторонних треугольников), 30 ребер и 12 вершин, которые являются местом стыка 5 ребер. Правильный икосаэдр из бумаги собрать достаточно сложно, но интересно. Если вы увлечены оригами, то сделать икосаэдр бумажный своими руками вам не составит труда. Его сделать из цветной, гофрированной бумаги, фольги, упаковочной бумаги для цветов. Используя разнообразные материалы, можно придать еще большую красоту и эффектность своему икосаэдру. Все зависит только от фантазии его создателя и подручного материала, имеющегося на столе.

Предлагаем вам несколько вариантов разверток икосаэдра, которые можно распечатать, перенести на плотную бумагу и картон, согнуть по линиям и склеить.

Как сделать икосаэдр из бумаги: схема

Для того чтобы собрать икосаэдр из листа бумаги или картона, необходимо предварительно подготовить следующие материалы:

макет икосаэдра;
клей ПВА;
ножницы;
линейка.

Во время создания икосаэдра важно обратить особое внимание на процесс сгиба всех деталей: для того, чтобы ровно согнуть бумагу, можно использовать обычную линейку.

Примечательно, что икосаэдр можно встретить и в повседневной жизни. Например, в форме усеченного икосаэдра (многогранник, состоящий из 12 пятиугольников и 20 шестиугольников правильной формы) выполнен футбольный мяч. Это особенно видно, если раскрасить получившийся икосаэдр в черно-белый цвет, как и сам мяч.

Такой футбольный мяч можно сделать самостоятельно, распечатав предварительно развертку усеченного икосаэдра в 2 экземплярах:

Создание икосаэдра своими руками представляет интересный процесс, который требует вдумчивости, терпения и большого количества бумаги. Однако результат, полученный в итоге, будет радовать глаз еще долгое время. Икосаэдр можно дать поиграть ребенку, если он достиг уже трехлетнего возраста. Играя с такой сложной геометрической фигурой, он будет развивать не только образное мышление, пространственные навыки, но и знакомиться с миром геометрии. Если же взрослый решил создать икосаэдр самостоятельно, то такой творческий процесс по конструированию икосаэдра позволит скоротать время, а также похвастаться перед близкими своим умением создавать сложные фигуры.